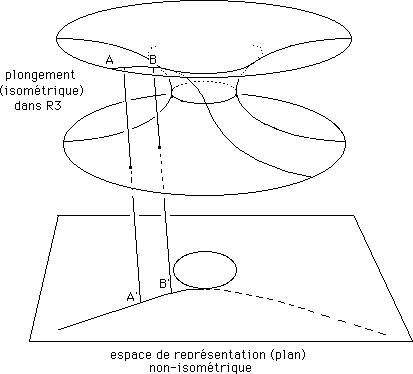

Ici, on a un peu "dégraissé" la figure pour la rendre plus lisible. Une surface est un objet 2d, ici "plongée" dans un espace 3d, euclidien, autrement dans dans R3. Au dessus, nous pouvons "la voir". Il se trouve que cette surface-là est plongeable dans cet espace R3 "de manière isométrique". C'est à dire que si on colle dessus un ruban de scotch, celui-cil s'inscrit effectivement sur une géodésique joignant deux points de la surface A et B. De plus, la longueur mesurée le long de cet arc géodésique est aussi correcte. C'est iso-métrique, étymologiquement "même longueur". En bas se trouve un espace de représentation 2d, qui donne une représentation qui n'est pas isométrique. La longueur de l'arc A'B' n'est pas égale à celle de l'arc AB. Fabriquez l'objet suivant, à l'aide d'une feuille de papier, d'un crayon et d'une paire de ciseaux :
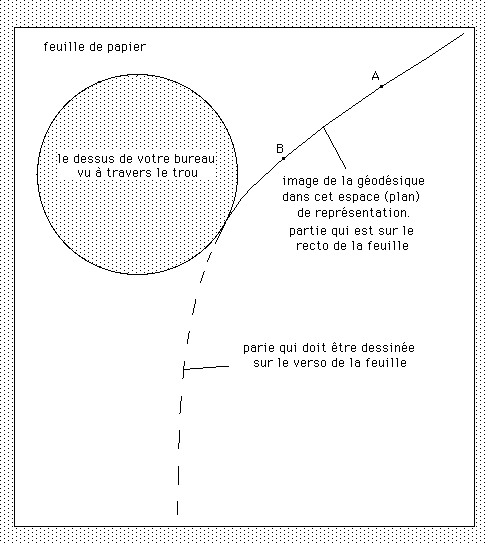
Ce dessin n'est pas isométrique . Primo la courbe indiquée n'est de toute évidence pas une géodésique du plan. Secundo la longueur de l'arc AB n'est pas "la vraie longueur", celle qu'on mesurerait sur "la vraie surface", qui "n'est pas trouée". Cette feuille de papier trouée n'est qu'une représentation commode, sans plus. De même que cette technique consistant dessiner un coup sur le recto de la feuille et l'autre sur son verso, l'ensemble de la courbe n'apparaissant qu'en transparence.
Sur le dessin ci-après on a figuré les géodésiques de cette surface, calculées par ordinateur (qui figure dans l'article).
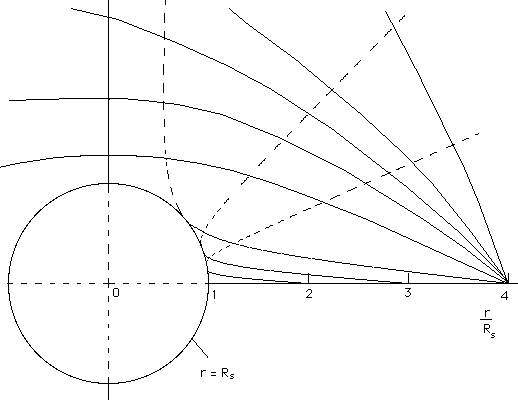
Les parties tiretées des courbes correspondent aux branches qui sont "de l'autre côté" (comme on on regardait la surface "par le dessus").
Maintenant, une question : puis-je construire une représentation plan et isométrique de ces géodésiques ? La réponse est oui. Nous avons vu que nous pouvions change la variable r en la variable r. Alors les géodésiques peuvent parfaitement être figurées dans un plan de "coordonnées polaire" ( r , j ). Les géodésiques (ici une géodésique non radiale) ont l'allure ci-après :
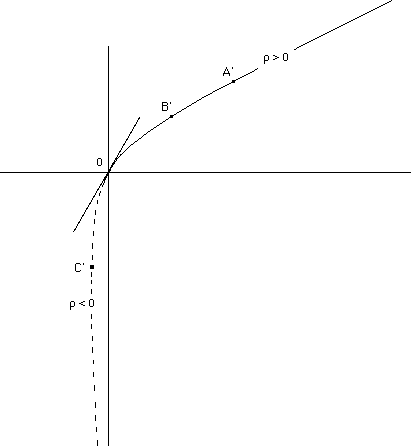
Cette représentation est isométrique. Soient trois point A , B , C appartenant à la surface, situés sur une même géodésique. A' , B' et C' sont les points homologues, dans cette représentation [ r , j ]. Les point A et B sont situés sur la même demie-nappe et l'arc géodésique qui les joint ne franchit pas le cercle de gorge. Mesurée dans ce plan, le long de l'image de cette géodésique (qui n'est évidemment pas une géodésique de ce plan), la longueur de l'arc A'B' est égale à celle de l'arc AB, mesurée dans la surface.
L'arc BC franchit la sphère de gorge. Même chose.
Mais cette isométrie ne s'applique pas à toutes les géodésiques de la surface. Il en existe une, unique en son genre : le cercle de gorge, réduit ici à un point C'est la seule géodésique de cette surface qui se referme sur elle-même.
Les géodésiques sont notre seule façon de comprendre une surface ou plus généralement un espace non plan, non euclidien. Ce sont des repères fiables (même si nous en avons des vision distordues à travers nos systèmes de représentation 2d ou 3d (en perspective). Ces géodésiques, nous savons qu'elles "existent", qu'elles sont intrinsèques. Celles d'une sphère sont par exemple de grands cercles. S'agissant d'espace-temps, ceux-ci sont peuplés d'une infinité de géodésiques spatio-temporelles. Ces géodésiques existent intrinsèquement et, pour comprendre (étymologiquement : enserrer, prendre dans ses bras) nous cherchons, comme des aveugles, à "palper" ces géodésiques. Mais les lignes de coordonnées de temps et d'espace n'ont aucune réalité intrinsèque, de même que les deux ensembles méridiens et parallèles ne font pas partie intégrante d'une sphère. Ils ne sont pas "livrées avec". La géométrie de Schwarzschild, solution de l'équation de champ d'Einstein, est une hypersurface 4d. Là-dessus les théoriciens ont plaqué des familles de courbes "à t constant", "à r constant", etc.
Gravez vous dans la tête que ces gestes restent totalement arbitraires. Mais même les spécialistes de cosmologie théorique perdent souvent conscience de ce point, que doivent leur rappeler de temps à autre les mathématiciens-géomètres. Il était donc parfaitement licite de changer de coordonnées d'espace et de temps.
A ce stade, vous me direz : mais alors, qu'est-ce qui permet de dire si tel choix de coordonnées est meilleur que tel autre ? Où se trouvent le raisonnable et le déraisonnable ? C'est une question de goût. Choisir des coordonnées d'espace et de temps, c'et plaquer une vision physique sur un objet mathématique. Dans le cas de la Terre, nous lui avons donné des pôles parce qu'elle tourne. Le pôle nord est simplement le point de la surface "Terre" dont la normale pointe vers l'étoile polaire, astre qui reste fixe dans la voûte étoilée.
A propos d'isométrie et de non isométrie, la cartographie illustre les problèmes qui résultent des tentatives de représenter une sphère sur un plan. La projection de Mercator (projection de la sphère terrestre sur un cylindre tangent le long de l'équateur) est très agréable pour les gens qui habitent près de l'équateur. Par contre l'habitant d'un des pôles a une mauvaise surprise : sn domaine, ponctuel, se transforme en droite...
Il y a trente six mille façons de projeter une sphère sur un plan. Imaginons celle-ci :
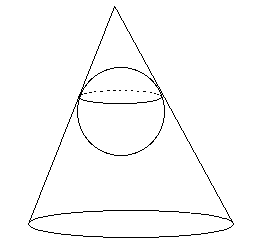
Imaginons que nous fabriquions des cartes géographiques sur ce modèle et nous les vendions. Succès immédiat auprès des habitants des deux pôles : ces projections sont alors, dans ces régions, quasi-isométriques. Très commode pour se faire une idée des distances dan ces coins-là. Si la Terre avait été habitable sur ses pôles et relativement inhospitalière ailleurs, les cartes auraient sans doute été créées de cette façon. On remarquera qu'alors le cercle frontière de la projection plane ne correspond plus à l'équateur, mais à un parallèle (ici appartenant à l'hémisphère nord). Au voisinage de cette région, la carte sera très loin de l'isométrie. De plus, sur cette carte bizarre, une partie du territoire devra être figuré en trait plein et l'autre en pointillé, puis qu'elle se situe au-delà de ce parallèle où l'objet, bizarrement, semble "se replier". A moins de fournir des cartes qui soient en forme de disques et où la suite du terrain figurerait sur l'autre face, sur le verso de la feuille.
Essayons de "penser tout cela en 3d". Nous avons représenté Lanturlu en train de plonger son bras gauche dans la sphère de gorge et nous avons séparés les deux dessins, ce qui semble évoquer le fait que ce second espace 3d puisse être "ailleurs". Pour être plus correct, il aurait fallu superposer les deux dessins en perspective en représentant la main (droite) qui émerge "en pointillé".
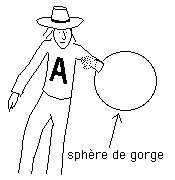
J'ai essayé de le faire, bien que ça n'ait pas été extrêmement facile. On aurait pu aussi utiliser deux couleurs différentes, par exemple rouge pour ce qui serait dans le premier versant 3d de notre espace 3d non simplement connexe et vert pour ce qui est dans l'autre versant. Un Lanturlu rouge verrait alors par exemple ressortir la main rouge, gauche, qu'il a plongée dans la sphère de gorge sous forme d'une main verte "droite".
Dommage que Raymond Devos ne s'intéresse pas aux maths. Quoique...
Evidemment "dans" la sphère de gorge, il n'y a rien. Cette apparence d'intérieur, de contenu volumique, n'est dû qu'au choix de cet espace de représentation 3d. De même qu'à l'intérieur du trou ménagé dans la feuille de papier il n'y avait pas de papier non plus. Ca n'était qu'un accident lié au choix de cet espace de représentation plan. Quelqu'un qui s'acharnerait à utiliser cette représentation plane sans enlever le disque découpé dans le papier et qui persisterait à demander "qu'y a-t-il dedans?" serait "à côté de la plaque" (ou plutôt... dedans). Cette plaque "n'existe pas".
Repassons en 3d. Quand Lanturlu plonge son bras dans la sphère de gorge, celle-ci n'a pas non plus d'intérieur. Cette apparence d'intérieur n'est dû qu'à ce choix d'espace de représentation. On pourrait considérer que Lanturlu et sa main émergeante ont été dessinés sur une feuille de papier possédant trois dimensions, où on aurait enlevé.. une sphère (équivalent 3d du disque de la feuille de papier). Mathématiquement, un disque est une "boule b2" et une "sphère volume" une "boule b3". On appelle "boule" une cellule contractile (voir le Topologicon, dans le "CD-Lanturlu") c'est à dire un objet qui peut se contracter selon un point en se parcourant lui-même. Ces exemples 2d et 3d sont là pour illustrer le plan d'attaque suivi dans l'article : la sphère de Schwarzschild n'a pas "d'intérieur", ni de "centre". Lorsqu'on la franchit (passage hypertorique) on se retrouve dans un "autre versant d'espace-temps".
Quelle est la justification de cette nouvelle interprétation de la "géométrie de Schwarzschild" ?
Réponse : l'élimination des singularités. Kruskal, avec son "prolongement analytique", a fait des pieds et des mains pour pénétrer à tout prix "dans" cette fichue sphère. Il n'a réussi qu'à tasser la singularité (rôle initialement tenu par la sphère de Schwarzschild) en un point situé "au centre de cet objet". On s'est contenté de ce tour de passe-passe. Mais nous pensons que sans singularité, c'est quand même mieux.
La Nature proteste, quand on la regarde sous le mauvais angle, en sécrétant des singularités. C'est comme ça que nous voyons les choses. C'est un point de vue a priori sur le "réel". Nous pensons que les singularités n'existent pas dans la nature. Nous pensons aussi que l'infini n'existe pas non plus. Mais, comme dirait Kipling, ceci est une autre histoire. J'ai eu avec Souriau des discussions agitées sur cette question il y a un an.
- Qu'est-ce qui me prouve que l'infini existe ? ....
- Mais, sans infini, il n'y a plus de mathématiques ! ....
- L'infini, tu l'a déjà rencontré ? Tu l'as déjà vu, tenu en main ?
- C'est une .... commodité.
- On engendre des nombres infiniment grands en supposant que l'on puisse ajouter 1 à un nombre, indéfiniment. Donc on se sert d'un infini séquentiel pour engendrer un infini numérique. Ca se mord la queue, ton truc.
- Bon, disons que c'est une commodité. L'homme a inventé deux choses importantes au cours de son histoire : l'infini et les chiottes....
Je ne crois pas non plus que l'infiniment petit existe, ni physiquement, ni mathématiquement. Mais cela fera l'objet d'autres papiers. Laissons pour le moment de côté ces questions. Simple digression.
Au passage, voir "Scale Invariant Cosmology" de P.Midy et J.P.Petit, International Journal of Modern Physics D, juin 1999, pages 271-280 où nous avons fait disparaître "la singularité initiale de l'univers". C'est une reformulation plus construite mathématiquement de l'idée que j'avais publiée en 88-89 dans Modern Physics Letters A (papiers sur le site).
J'espère que quand vous lirez ces lignes nous aurons eu le temps, avec l'aide des sieurs Lecot ou Boland, d'inclure ce nouvel article dans le site. Mais de toute façon, même si ce travail s'y trouvait reproduit, ne vous y aventurez pas. Comme avait inscrit je crois Archimède à l'entrée d'un sanctuaire-science "nul n'entre ici qui ne soit géomètre". C'est tenseurs et compagnie, domaine dans lequel Midy se régale, mais c'est aussi indigeste que du pudding anglais.
On voit donc, à travers ce discours, que la vision physique que nous avons des phénomènes est issue de la façon dont nous avons décidé de nous les représenter. Nous avons, en modifiant les coordonnées spatiales, changé de "topologie locale", mot qui mériterait à être précisé mathématiquement, dit Souriau. En fait, cette phrase est un doux euphémisme : il s'est simplement mis à hurler quand j'ai prononcé ce mot. Son chat Pioum et moi avons eu toutes les peines du monde à le calmer. Souriau, c'est le Tournesol des mathématiques. Il pratique volontiers l'indignation mathématique portée à son comble. Mais ces accès d'indignation ne sont pas à confondre avec la colère au sens trivial du terme. Je serais plutôt "Monsieur Jourdain", dans ce domaine. Les physiciens font souvent des mathématiques sans le savoir (et vice-versa d'ailleurs).
En admettant, provisoirement, l'usage de mots "non précisés", tout se passe comme si on avait considéré jusqu'ici que la "topologie locale" de la géométrie de Schwarzschild était "hypersphérique (que la sphère de Schwarzschild "contienne" une "boule b3"). Nous l'avons rendue "hypertorique". C'est la raison pour laquelle j'ai proposé l'appellation (non contrôlée) de "géométries hypertoriques".
On a évoqué plus haut l'inversion de l'espace. Cela se négocie avec les groupes. Peut-on comprendre cela autrement ? On a vu que Lanturlu, plongeant son bras gauche dans la sphère de gorge, voyait ressortir ... une main droite. En fait, chaque atome de sa main a suivi une géodésique "radiale", dirigée perpendiculairement à la surface.
Remarquons au passage, nous avions oublié de le dire, que ce mode de représentation n'est pas isométrique. Comme pour le coup du papier troué, tout à l'heure. Si on mesurait la longueur parcourue par un atome-témoin appartenant à la main de Lanturlu dans les deux demi-espaces, ceci ne coïnciderait pas avec la véritable longueur qu'on peut calculer avec une ficelle.
Reprenons une dessin donné plus haut.
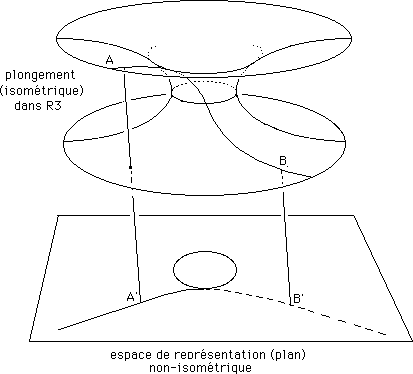
Ici, nous avons figuré un arc géodésique AB qui franchit le cercle de gorge, et son image dans l'espace de représentation plane, en bas. Le caractère de représentation non isométrique apparaît alors encore plus clairement. Les longueurs des arcs AB et A'B' sont très différentes.
Il est évidemment assez difficile d'imaginer que l'on puisse enfiler une ficelle dans la sphère de gorge d'un passage hypertorique. En tendant la ficelle, on obtiendrait d'ailleurs une géodésique (ligne de plus court chemin). Au demeurant, si on mesurait la longueur de cette ficelle dans l'espace de représentation 3d (Lanturlu qui enfile son bras) et qu'on s'aventure à mesurer la longueur de ladite ficelle, dans cet espace, on trouverait une longueur A'B' plus courte. La véritable longueur, mesurée dans l'hypersurface 3d, serait plus longue, comme figurée ci-dessus en 2d. La représentation 3d où figure Lanturlu est donc non-isométrique, comme la représentation plane de la figure ci-dessus.
Au fond, ces concepts si subtils, issus de la théorie des groupes, finissent par devenir moins hermétiques, grâce à quelques dessins, à condition de "voir dans l'espace". Ce que je suis en train d'essayer de vous apprendre, c'est à voir dans un espace 3d courbe.
Revenons à cette affaire d'énantiomorphie, d'inversion des objets quand ils franchissent la structure de gorge, en 2d ou en 3d. Envisageons, en 2d, des géodésique "radiales". Le mot est devenu impropre puisqu'un rayon est en principe une droite qui part d'un point. Il s'agit en fait de géodésiques à j constant. Voir une figure, plus haut, où cette coordonnée azimutale a été indiquée. Mais, pour plus de concision nous continuerons à utiliser le mot "radial" en utilisant des guillemets. Remarquez que ce mot "radial" est encore une retombée du choix d'un espace de représentation. Imaginez qu'une lettre R (laquelle n'est pas identique à son image en miroir, à son image énantiomorphe) glisse, comme une décalcomanie mal collée, le long de notre passage torique, chacun de ses points cheminant selon une géodésique. Cette lettre va se retrouver "de l'autre côté". Ce qui est intéressant c'est de regarder le résultat de l'opération dans la projection plane, dans l'espace de représentation.
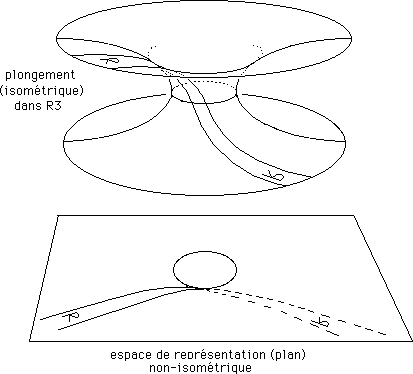
On a représenté une sorte de ruban, dont les bords sont constitués par deux géodésiques. Que constate-t-on ? Dans l'espace de représentation, la lettre R s'est inversée, est devenue un "ia" russe, un R à l'envers, énantiomorphe. On commence à comprendre maintenant pourquoi la main de Lanturlu, en ressortant dans "on "espace de représentation 3d" semble s'être inversée, est devenue énantiomorphe.