^{For correspondance :}

________________________________________________________________

Abstract

    Starting from the so called black hole model, considered as a physical interpretation of Schwarzschild geometry, we reconsider the problem of the fate of a neutron star when it overcomes its limit of stability. We first present a new geometric tool : hypertoric geometry, through 2d and 3d examples (section 2). We show that pathlogies associated to metrics, arising from their line element expressed in a given coordinate system can be cured through a more suitable choice phrased in terms of "local topology". For example we show that in the two given examples, the 2d surface and 3d hypersurface, whose isometry groups are O2 ans O3, are not simply connected.

    We extend the method to Schwarzschild geometry. We show that singular features can be fully eliminated, considering not simply connected space time hypersurface. We give the Schwarzschild geometry a different physical significance : a bridge linking two universes, ours and a twin universe.

    We show that the "freeze of time", keystone of the black hole model, is a simple consequence of an arbitrary peculiar time marker choice. Using another one, inspired by Eddington's work (1924) we derive a completely different scenario, implying a radial frame dragging (similar to the azimutal frame dragging of the Kerr metric). We show that the Schwarzschild solution can be interpreted as a "space bridge", linking two universes, two space-times, working as a one way bridge. We show that the transit time of a test particle is finite and short, which immediately makes the classical black hole model questionable.

    Extending the isometry group of the Schwarzschild metric we show that the two universes are enantiomorphic (P-symmetric) and own opposite time markers
(t* = - t). Using a groups' tool : the coadjoint action of a group on its momentum space, we give the physical significance of this "time inversion", through the spherical throat surface, the Schwarzschild sphere : when a positive mass particle passes through the space bridge, its contribution to the gravitational field is inversed : m* = -m (as shown by J.M.Souriau in 1974, the inversion of the time marker is equivalent to mass and energy inversions).

    As the question of the fate of a destabilized neutron star becomes a still open problem, we present a project of an alternative model : the hyperspatial transfer of a part of its matter, through a space bridge, this matter flowing towards the twin universe at relativistic velocity.

    By the way we recall some well-known defects of the Kruskall model, particularly the fact that it is not symptotically Lorentzian at infinite.

    We suggest to consider Schwarzschild geometry as an hypersurface imbeded in a ten dimensional space. Linking the present work to former ones, based on group theory, we build a CPT symmetric model. The matter antimatter duality holds in both folds When matter is transfered towards twin Unverse, it undergoes a CPT-symmetry and its mass (its contribution to the gravitional field) is reversed. But its is still matter. Similarly, antimatter flowing in space bridge remains antimatter, with opposite mass, for the inversion of the time marker, as shown by Souriau, implies the inversion of the mass.

________________________________________________________________

1) The black hole model.

  Neutron stars cannot exceed a critical mass, close to 2.5 solar masses. For higher masses, their material cannot stand any longer the huge internal pressure due to gravitational force. Then gravitational collapse occurs. For a long time, theoreticians tried to describe the fate of such an object. Looking at the Schwarzschild metric, hereafter expressed in terms of

coordinates, where Rs is the so called Schwarzschild radius

(1)

people imagined that this solution of the Einstein's equation :

(2)

with zero second member could solve the problem. In effect, if t is chosen as " the cosmic time of an "external observer", the free fall time of a test-particle, following a "radial geodesic", from any distant point from the Schwarzschild sphere r = Rs is found to be infinite, while this free fall time Ds, expressed in proper time remains finite. Then the "physical description" is the following :

- The object (a neutron star which overcomes its limit of stability) undergoes a gravitational collapse. Its mass falls rapidly towards "the geometric center of the system", described as a "central singularity". This phenomenon extends over a finite duration Ds, in terms of proper time s.

- But, for an "external observer", located at some distance from the object, this process looks to be "frozen in time". Furthermore the Schwarzschild sphere is an infinite redshift surface (due to the nullity of the g_tt term of the metric at r = Rs).

This is the model of a spherically symmetric black hole.

r is identified to a "radial distance", which means that one can think about "what's inside the Schwarzschild sphere". Roughly speaking, it means that one assumes that the "local topology" is "spherical" : Inside the Schwarschild sphere, a "smaller sphere is supposed to be located", an so on, up to the "geometrical center" of the object.

    Later the model was extended to axially symmetric geometry (Kerr metric). But this extension brings no fundamental conceptual change. That's for we are going to concentrate in the following on spherically symmetric system (we think that this study could be later extended to the Kerr metric).

    It is a little bit strange that such very dense object can be decribed through a solution of equations (2), which a priori refers to an empty portion of the Universe where there is no matter-energy.

    If one keeps the

description (a peculiar choice of coordinates), many difficulties arise. For example, when r tends to Rs the g_rr term tends to infinite.

The signature of the metric, expressed with this peculiar choice of coordinates is :

When a test particle penetrates inside the Schwarzschild's sphere its mass becomes imaginary and the its velocity larger that the light velocity : it becomes a tachyon.

Considering the change of signature, some people said :

- No problem : Inside the Schwarzschild's sphere r just becomes the time an t the radial distance.

    A french cosmologist, Jean Heidmann, uses to say : "when we think about black holes, we have to give up any common sense".

    By the way, they are very few black hole candidates, which is the most the more puzzling point. In effect, supernovæ, white dwarfs and neutron stars where predicted before they were observed. Ford example, Fritz Zwicky presented the supernova model, in a famous lecture given in Caltech in 1931 before anyone was observed. But years after years the model was confirmed and we now known hundreds of them. Same thing for rotating neutron stars, identified to pulsars. Why so few observed black holes ?

    Anyway, astrophysicists believe than black holes do exist, even if ther is so few observational data about them. They "use" models of "giant black goles", supposed to be located at the center of galaxies or clusters of galaxies, to "explain" some of their puzzling dynamicals features.

In the following, we would like to suggest a different fate for neutrons stars which overcome their limit of stability. Let us start to introduce new geometrical tools.

2) Hypertoric geometry.

Consider the following riemanian metric g , in two dimensions, whose line element, written with a set of two coordinates [ r , j ] is :

(3)

where :

is defined on R, modulo 2 .

Rs is a constant.

This metric becomes asymptotically euclidean when r tends to infinite :

(4)

In this peculiar

coordinates system the signature is :

The determinant :

(5)

becomes infinite for r = Rs . Let us show that this is due to this peculiar choice of coordinates. Introduce the following change of coordinate :

(6)

The line element becomes

(7)

whose associated determinant is :

(8)

It no longer vanishes for all values (which by the way shows that, in a metric, the nullity of the line element's determinant depends on the choice of the coordinate system, as evidenced by Eddington in 1924 (ref.[10]) for Schwarzschild's metric). When    tends to zero (which corresponds to

this determinant tends to :

varies from - infinite to + infinite which is equivalent to r ³ Rs

    The metric g ,whatever the chosen coordinates system is, describes a surface, a two dimensional object. This last owns its geodesic system, basically coordinate-invariant. Let us study this system in a

coordinates system through Lagrange equations system. Introduce the following F function :

(9)

The corresponding Lagrange equations are :

(10)

(11)

The equation (11) gives :

(12)

h being positive, negative or zero. In addition if in (3) we divide the two members by , we get, classically :

(13)

from which we may derive the differential equation which describes the plane geodesics, in the

coordinates system :

(14)

The condition IhI £ r , according to (12), means that the absolute value of the cosine of the angle between the tangent to the geodesic and the radial vector is £ 1.

Now let us imbed the surface in R3, adding an imbedding additional coordinate z. We choose cylindrical coordinates

The surface is axisymmetric with respect to the z-axis.

The (    = constant ) geodesics are the meridian lines of this surface, where :

(15)

which immediatly gives the equation of the meridian curve of this surface, as imbedded in R3. It is the parabola :

(16)

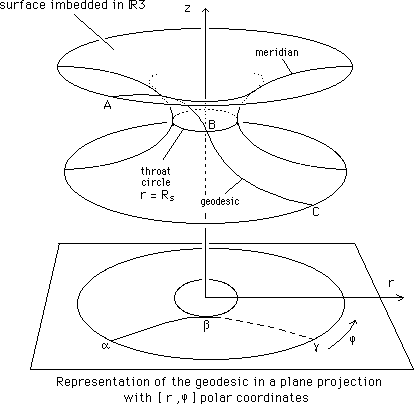
Figure 1 shows a 3d view of this surface, as imbedded in R3, plus one geodesic and its projection on a plane with

polar coordinates.

This surface is not simply connected. Among the orbits of the isometry group O2 we find a minimum perimeter circle: the throat circle (p = 2 Rs).

On figure 2 several geodesics are shown, in this

representation system.

Fig. 2 : representation of some geodesics.

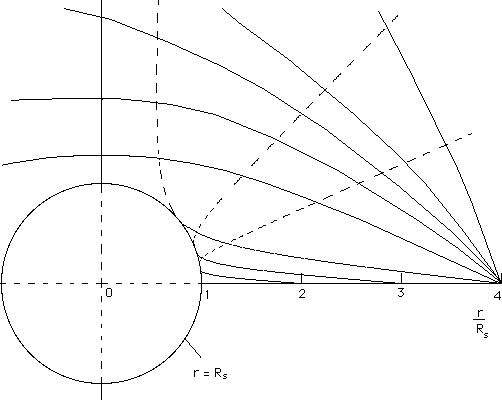
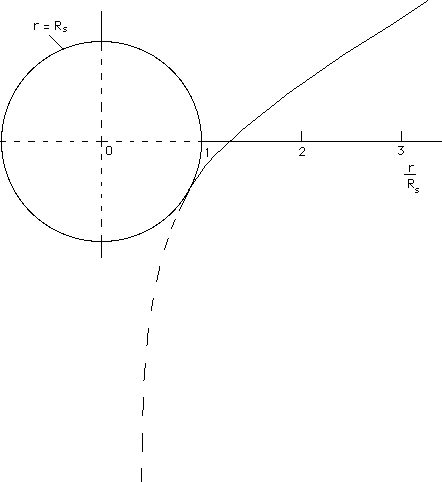
    Notice that this representation of geodesics in a plane

is not isometric. Is we measure the length on this plane, it does not correspond to the length as measured on the surface.

    If we impose the length dS to be real, we see that it determines what we could call the local topology . Let us call such geometric structure a toroidal bridge . We can also say that this surface owns a local toroidal topology . It owns a single fold, which can be considered as a set of two bounded half-folds, the two being glued along their circular borders along the throat circle, whose perimeter is 2 Rs . These circles are not geodesic lines (except thhis very peculiar geodesic which is the throat circle, the only closed one). On each half-fold, when the distance with respect to the "toroidal bridge" tends to infinite the metric tends to the euclidean one (2). On the figure 2, corresponding to a [ r ,  ] representation, the upper portions of the geodesics crossing the throat circle have been figured as a continuous lines, while the portions corresponding to the other half-fold have been figured as dotted lines. Notice that one half-fold corresponds to ( ) , whence the other corresponds to ( ) . The throat circle corresponds to = 0 .