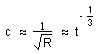
COSMOLOGICAL MODEL WITH VARIABLE LIGHT VELOCITY :
THE INTERPRETATION OF RED SHIFTS.
Jean-Pierre PETIT.
Observatoire de Marseille
Modern Physics Letters A, Vol.3 , n° 18, dec. 1988, p.1733
ABSTRACT :
cThe model with variable c, G, h presented in reference [1] is extended to electromagnetism. The entropy is found to vary like Log t and, in a space-entropy representation, the metric is conformally flat. A new gauge relation is suggested, based on geometrical considerations, which corresponds to a Rydberg constant varying like R. The Hubble's law still applies. The age of the universe is unchanged while its span is found to be half of the Mattig's value. The complete decoding of the red shift can be done. The distances of the sources are very similar. The large volumic power densities of distant quasars could have been greatly overestimated, while the increase of their absolute magnitude, as derived from the classical theory, could be due to the secular variation of c. Assuming the electron-proton mass ratio to vary like R we get a fine structure constant a, a Bohr radius and a ratio electromagnetic force to gravitational force which behave like absolute constants.
1 - INTRODUCTION
...Several authors tried to develop models with physical constants in time varying in time [2, 3, 4, 5, 6, 7, 8, 9] . None questionned the light velocity c, always considered an absolute constant. If one wants to save the form of the conservation equations, the Einstein's constant c = - 8 p G / c2 must be considered as an absolute constant. In such conditions if one wants to keep the light velocity c as an absolute c constant and a variable gravitational constant G, one must add a source term to the field equation, see reference [3] . Thus, all these theories imply a constant creation of matter.
...In a previous paper [1] we showed that a variable ligth-velocity could lead to a consistent model if both G and the Planck's constant h followed convenient gauge relations. Thus, the constant creation of matter was no longer necessary. The extension of the Robertson-Walker metric to a variable light velocity configuration and its introduction into the field equation gave a complete set of gauge relations. Let us recall the main features of the model described in [1] :
(1)
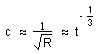
(2)
m ( particle's mass ) »
R
(3)
h ( Planck'constant ) »
R3/2 »
t
(4)
G ( Gravity constant ) »
1/R
(5)
R ( Characteristic length ) »
t 2/3
(6)
V ( Velocity of a free particle ) »
R-1/2 »
c
(7)
r ( mass density )»
1/R2
(8)
mc2 = constant
The following is a short digression about entropy.
2) TIME OR ENTROPY ?
The relativistic formulation of the velocity distribution function is :
(9)
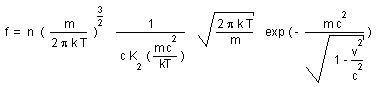
where m is the rest mass,
T the temperature, n the number of density and K2 a Bessel function.
If b
= (<v2>1/2/c) << 1 then we get the classical
Maxwell-Boltzmann velocity distribution function :
(10)
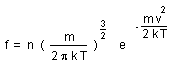
Let us compute the entropy
per baryon, as defined by :
(11)
![]()
where k is the Botzmann's
constant. We have n »
R-3 , m
»
R and R »
t2/3,
T = constant ( see reference [ 1] ) , such as :
(12)
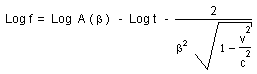
Then :
(13)
s = k Log t + H( b )
In the model b is gauge invariant such as s » Log t.
...In the classical cosmology the universe is isentropic. One could consider somewhat paradoxal that such enormous change in time goes with an almost zero entropy variation. In the new model the entropy grows with time. Notice that the BIG BANG singularity corresponds to s = - ¥ .
Let us define now the entropy
through :
(14)
s = 3/2 k Log t
Let us return to the Robertson-Walker
metric
(15)
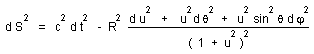
We get :
(16)
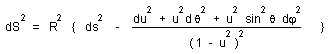
...In the representation { entropy, space variables } the metric is conformally flat. From a cosmological point of view, the entropy (which on another hand is invariant with respect to the Lorentz transform ) could be a better choice than time.
...In addition, if we describe the universe in a phase space ( position plus velocity ) we find that the associated characteristic hypervolume R3c3 varies like t.
3) THE RED SHIFT AND THE ROBERTSON-WALKER METRIC :
...Consider a radiating object, say a nebula N1, which could be considered as a particle. Suppose his light is observed on a nebula N2 placed at the origin of the co-moving coordinates. The nebula N1 is characterized by the value of its time-independent distant marker z, defined by the relation :
(17)
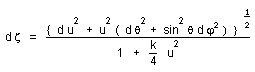
The light emited at time t1 is observed on N2 at a time t2 with t2 > t1 .
The distance between N1
and N2 is R(t) dz and
is time-dependent but
dz
is not. Light travels on a nul geodesic :
(18)
ds2 = (dx°)2 - R2 dz 2= o
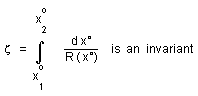
Consider the light emited
by N1 at a corresponding value
x°1 + D x°1 of the chronological parameter. It will
be received at
x°2 + D x°2, where it will be determined through
the relation :
(19)
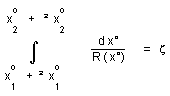
...Consider
D x°1 as the equivalent of the period of some physical
phenomenon, the emission of radiation for instance, taking place on N1 , and
Dx° to be short compared to the equivalent of the
travel time from N1 to N2 ( in term of chronological parameter x° ). The periodic
phenomenon will appear, as seen from N2 , to have a "period" D
x°2 which, from the above relation, will be such that the increment of the q
integral will be zero. This, by elementary calculus, gives :
(20)
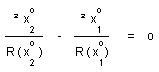
Let us introduce the cosmic time t as defined before through dx° = c dt and write R (x°1) = R1 , R(x°2) = R2 , c (x°2) = c2 , c (x°1) = c1 , then we get :
(21)
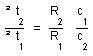
4) THE PROBLEM OF ELECTROMAGNETISM :
...Now
we cannot assert that the energy Ei(t1), emitted by the atom at the time t1
would be identical to the corresponding emission energy Ei(t2) of a similar
atom, at time t2, in lab's conditions. The light emission is an electromagnetic
process. Everybody knows that the classical field description, applying to a
four dimensional space time does not take in charge the electromagnetic phenomenon.
To get a complete description of universe gravitation and electromagnetism should
be imbedded in a common geometrical framework. Unfortunately it has not been
done yet in a satisfactory way so that our work will now loose somewhat its
self-consistency. . Suppose, for instance, that the Rydberg constant ( ionization
energy of hydrogen ) would simply obey the following hypothetic gauge relationship
:
(22)
Ei » Rg
( Notice that this is a totally arbitrary assumption ). Let us explore the consequences of it on the red shift decoding. Later we will try to relate it to possible gauge relations.
5) THE RED SHIFT PHENOMENON :
...In the classical description the red shift z is due to the Doppler effect, plus some special relativity additional effect. The indix 1 refers to the emitter and the indix 2 to the receiver. For a given specctroscopic line, call E1 = h1n1o the emission energy and E2 = h2n2o the corresponding emission energy in the today's lab's conditions, for the same line. The light is emitted by an atom at rest at the frequency n1 = n1o, corresponding to the wavelength l1 = c1/n1 = l1O.
n2 will be the mesured reception frequency, with l2 = c2/n2 and l2o = c2/n2o . The energy of any radiative process will follow the general assumed gauge law (22).
We can define the red shift z :
- As the ratio between the wavelengths :
(23)
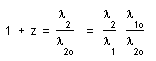
(24)
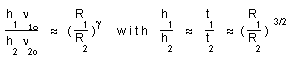
(a)
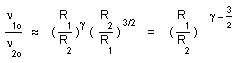
(b)
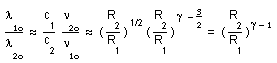
(c)
then we get :
(25)
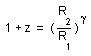
Notice that, for g = 1 we refind the classical model.
- As the ratio between the frequencies :
(26)
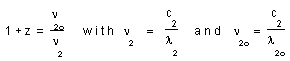
we get the same result.
- As the ratio between the energies.
(27)
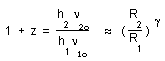
same thing. The classical relation suggests the choice g = 1 .
6) THE HUBBLE'S LAW AND THE ROBERTSON WALKER METRIC :
Let us expand the function 1/R(t) into a series with respect to
(28)
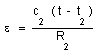
we get :
(29)
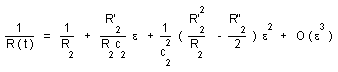
In R'2 and R"2 the prime denotes differentiation with respect to t.
In particular , at the first order :
(30)
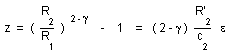
Next, expanding the following expressions :
(31a)
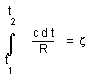
(b)
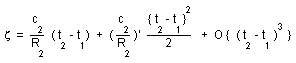
(c)
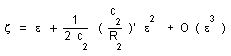
Refering to the first order :
(32)
![]()
As a first approximation the astronomer measures d2 @ R2 z, such as :
(33)
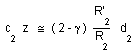
Which is nothing but the Hubble's red shift law, which still applies in this variable light velocity conditions. From mesurement of d2, c2 and z we can derive the so called Hubble's constant, i.e. the age of universe.
Take R = 3/2 c t ( see reference [ 1) ).
(34)
![]()
The age of universe corresponds to :
(35)
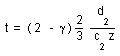
A g = 1 value gives the standard model value.
7) THE RED SHIFT AND THE DISTANCE EVALUATION :
Let us return to the Robertson-Walker metric, which provides :
(36)
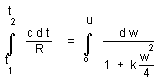
In the classical approach, take the Einstein-de Sitter model
( k = o ). We get :
(37a)
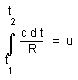
With R = a t2/3 we have :
(b)
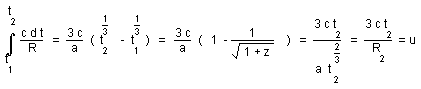
whence
(38)
![]()
If z is weak : d2 » 3/2 ct2 z
if z tends to infinite : d2 tends to 3 c t2
Of course the Mattig's formula gives the same result :
(39a)
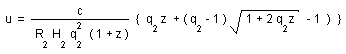
(b)
![]()
(c)
![]()
Let us return to the Robertson Walker metric, following our model, with k = - 1 :
(d)
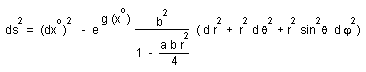
write :
(e)
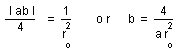
(f)
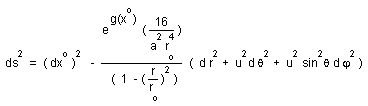
Let :
(g)
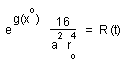
Then :
(h)
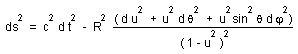
For radial pathes :
(i)
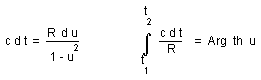
(j)
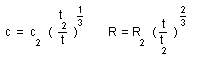
Log ( 1 + z ) = Arg th u
(k)
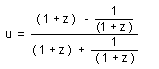
(l)
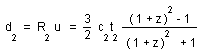
When z tends to infinite we refind the horizon (3/2)c2t2, which is twice smaller than the standard value 3 c2t2 .
Notice this is completely similar to the law giving vr/c ( where is the radial velocity ) as a function of z, ine the standard model.
Let us compare the distances, as given by our model and the standard model.
(40)
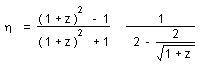
They are similar for weak z values.
8) THE QUASARS PROBLEM :
...Quasars correspond presently to z values from 0.13 to 4 . The diameters of the quasars are estimated from their fluctuation period T. We get a maximum diameter cT. With respect to the standard approach this model gives larger values, for c was larger in the earlier time.
...The volumic power is refered to the size of the galaxies. Call PQSO the absolute power emited by a quasar and PG the absolute power emited by a galaxy. The relative power density of the QSO, with respect to a galaxy, is :
(41)
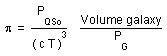
- Change for the distance ( they are a little bit closer ).
- Change for the diameter ( due to the variation of c ).
- Change of the galaxy's size.
Given PQSO and PG the coefficient (57) becomes p' = p x with :
(42)
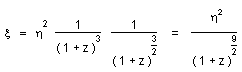
i.e :
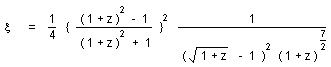
(43)
|
z |
h |
x |
|
|
0 |
1 |
1 |
|
|
0,13 |
1.025 |
0,606 |
The closest quasar |
|
0,2 |
1.03 |
0.467 |
|
|
0.5 |
1.048 |
0.177 |
|
|
1 |
1.024 |
0.0463 |
|
|
1.5 |
0.985 |
0.0157 |
|
|
2 |
0.946 |
0.0063 |
|
|
2.5 |
0.912 |
0.00296 |
|
|
3 |
0.882 |
0.00152 |
|
|
3.5 |
0.856 |
0.000842 |
|
|
4 |
0.834 |
0.0005 |
The most distant quasar |
|
5 |
0.8 |
0.000201 |
|
|
6 |
0.771 |
0.0001 |
|
|
7 |
0.75 |
0.0000485 |
|
|
8 |
0.731 |
0.0000275 |
|
|
9 |
0.71 |
0.0000162 |
|
|
10 |
0.7 |
0.0000102 |
...We see that this correction reduces the absolute magnitude of the observed quasar, and that this correction increases with z. Thus, would this model would be good, the classical model would have greatly overestimated the volumic power density of quasars. In addition the observed increase of absolute magnitude of quasars could be due to the secular change in c.
Classically the galaxies' span are related to the Jeans' length, but the model does not provide any avaible information about the sizes of some emitting objects like stars or quasars. It depends on the energy emission process. As we have not defined some possible gauge relation for the fusion coefficients we have no avaible model yet. Anyway the quasars could grow in time, like galaxies and the observations tend to support this hypothesis, that will be examined with more details in the next paper devoted to the detailed interaction of the model and avaible observations. .
9) ASSOCIATED GAUGE RELATIONS.
...The ionization energy of hydrogen obeys : Ei = 1/2 a2 mec2, where a is the fine structure constant and me the mass of the electron. We have assumed that Ei » Rg with g = 1, in order to fit with the classical model, see (25), (33) and (35). Introduce the electron-proton mass ratio d = me/mp . According to the first paper [ 1] mp » mn » m » R. So that mc2 is an absolute constant. Then :
(44)
![]()
...The fine structure constant a and the electron-proton mass ratio d cannot be kept constant together. We shall consider two possibilities ;
9.1) Let us take first d » constant. Then :
(45)
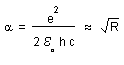
Introducing the gauge relations for h and c we get : e2 /eo » R3/2 and the electromagnetic force Fem =e2 /4peoR2 » R-1/2. Then :
(46)
![]()
which is similar to an old idea of Dirac [ 4, 5] .
Let us compute the Bohr radius :
(47)
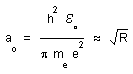
9.2) Now we take a » absolute constant. Then me » R2. and
e2 /eo » R. The Compton length of the electron h/mec, the ratio gravitational force to the electromagnetic force and the Bohr radius become absolute constants.
...In the references [10] to [13] several authors study the possible variability of several quantities : a, a2(gp/ge)(me/mp) , me/mp ,where gp and ge are the gyromagnetic ratios of the proton and the electron. Following B.E.G. PAGEL [13] , we have :
|
Effect |
Quantity Approximate 3s upper |
limit to variation. |
|
Optical doublet splitting. |
a |
3 % |
|
Comparizon of optical and 21 cm redshifts. |
a2(gp/ge)(me/mp) |
10-3 |
|
Comparizon of hydrogen and metal redshifts. |
d = me/mp |
50% |
...As a consequence we choose the second possibility, with a variable mass ratio. Notice that in both cases we get gp/ge » 1/R.
1O) CONCLUSION
...Here we tried to extend the model introduced in reference [1] to electromagnetism. A gauge law was suggested : we assumed the ionisation energy Ei ( Rydberg constant ) to vary like Rg. Local geometrical considerations recommand the value g = 1 , which takes account of the desonization process during the cosmic evolution. The distance of a radiative source, as derived from the Robertson Walker metric, gives results quite similar to the standard model'values, but this new model tends to reduce considerably the estimated density power of distant sources like quasars. In addition the increase of absolute magnitude in z, as derived from the classical model, could be due to the secular variation in c.
...With an electron-proton mass ratio d = me/mp which varies like R we get a fine structure constant a which behaves like an absolute constant.
REFERENCES :
[ 1] J.P.PETIT : An interpretation of cosmological model with variable light velocity. Modern Physics Letters A......
[ 2] E.A. MILNE : Kinematic Relativity Oxford 1948.
[ 3] F.HOYLE & J.V.NARLIKAR : Cosmological models in conformally invariant gravitational theory. Mon. Notices Roy. Astr. Soc. 1972 155 pp 3O5-325.
[ 4] P.A. DIRAC : 1937, Nature, 139,323
[ 5] P.A. DIRAC : 1973 Proc. Roy. Soc. London , A333, 4O3
[ 6] V.CANUTO & J.LODENQUAI : Dirac cosmology, Ap.J. 211 : 342-356 1977 January 15.
[ 7] T.C.VAN FLANDERN : Is the gravitational constant changing ? Ap.J, 248 : 813-816
[ 8] A.JULG. Dirac's large numbers hypothesis and continuous creation. Ap.J. 271 : 9-1O 1983 August 1
[ 9] V.CANUTO & S.H. HSIEH : The 3 K blackbody radiation, Dirac's large numbers hypothesis, and scale-covariant cosmology. Ap.J., 224 : 3O2-307, 1978 September 1
[ 10] B.E.J.PAGEL : On the limits to past variability of the proton-electron mass ratio set by quasar absorbtion line redshifts. Mon. Not. astr. Soc. (1977), short communication, 81P-85P.
[ 11] A.M.WOLFE & R.L.BROWN & M.S.ROBERTS. Limits on the variation of fundamental atomic quantities over cosmic time scales. Physical Review Letters Vol 37, number 4, 26 July 1976.
[ 12] A.D.TUBBS & A.M.WOLFE : Evidence for large-scale uniformity of physical laws. A.P.J, 236 : L1O5-1O8, 198O March 15
[ 13] B.E.J.PAGEL. Implication of quasar spectroscopy for constancy of constants. Phil. Trans. R. Soc. Lond. 3 31O, 245-247 , 1983.
