Abstract :
Starting from the two coupled field equation and assuming separate conservations equations, due to zero divergence conditions, the susbsequent coupled Euler equations systems ins analyzed, which gives two coupled Jean's equations. A solution is given, which evidences the joint gravitational instabilities effect.
1) Building a coupled Jeans' equations system.
In references [1] to [9] we have developped a model based on the two coupled field equations system.
(1)
(2)
We assume these equation to be
divergenceless, which gives :
(3)
It gives conservation equations.
In the general case it means that the energy-matter is conserved over the
two folds, if one admits that some material can be transfered from a fold
to the other, through some hypertoric bridge. At the present time we do not
deal with such process and shift to the more restrictive form :>
(4)
which means that the energy-matter
is conserved in the two folds, in the two sub-systems : matter and ghost matter.
Then we separate conservations equations. We write the equations in a common
system of coordinates { t , x , y , z }, of an observer located in the fold
F.
Matter and ghost matter obey distinct sets of Euler equations :
(5)

(6)
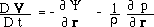
(7)
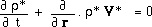
(8)
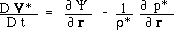
We can add :
(9)
Starting from steady initial conditions
:
(10)
r* = r*o
T = To
T* = T*o
V = V* = 0
we use a perturbation method,
with the perturbed Poisson equation :
(11)
Introducing the Jeans lengths :
(12)

we get two coupled Jeans equations
:
(13)
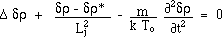
(14)
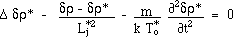
which describe the joint gravitational instabilities phenomenon.
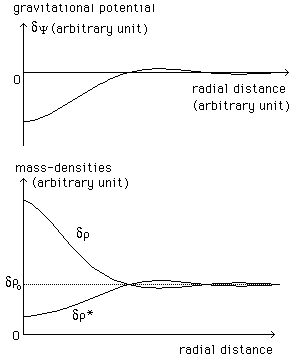
Imagine now that we deal with a spherically symmetric steady state system, corresponding to a final state.
We can describe it by two maxwellian
distribution functions f and f* (thermodynamic equilibrium). Then we know
that the mass-densities obey :
(15)
![]()
that are introduced in the Poisson equation.
![]()
Write it in an adimensional form, with :
(16)
we get :
(17)
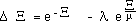
with is solved numerically on figure 1, for l = m = 1 ( ro = r*o )