 |
2
|
 |
2
|
Any element of the group
must own its inverse , written g-1 , defined by :
(15)
In our example :
(16)
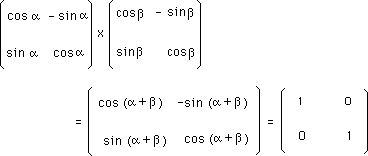
i.e : b
= - a or :
(17)
Here the calculation of the inverse matrix is trivial.
What is the condition for a given square matrix to own its inverse ?
...To any square matrix we can associate a scalar called determinant . For definition see any book devoted to linear calculus . This determinant is codified : det ( g )
In addition we have a general theorem :
The determinant of a
diagonal matrix is :
(18)
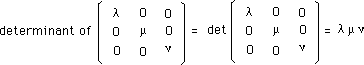
As a consequence :
for 1 is a diagonal matrix.
From the definition of
the inverse of a matrix :
Then :
(19)
...If
det (g) = 0 the condition (19) cannot be satisfied. Sets of matrixes
whose peculiar elements own null determinant don't satisfy the third axiom,
and cannot form a group.
By the way :
(20)
4 - Fourth axiom of groups'theory :
The multiplication must
be associative, i. e : .
(21)
Matrix multiplication
is basically associative.
Dimension of a group
:
...As
we will see, a group may act on a space whose points are described by column-vectors.
For an example space-time points (called "events") :
(22)
...This is a four dimensions space. Different groups may act on it. But the dimension of a group has nothing to do with the dimension of the space it acts on.
We have given an example of matrixes, defined by a single parameter
So that the dimension
of this group is one.
Notice that :
(22-bis)
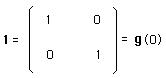
Remark :
All groups of matrixes
are not commutative , although the group we studied owns this property
:
(23)
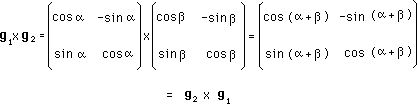
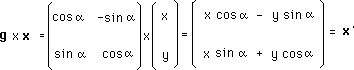
it corresponds to rotation around a fixed point, in a plane :
(23 ter)
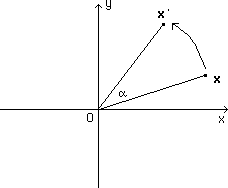
This operation is obviously commutative.
You will tend to say : "like all rotations groups".
...You're wrong. Consider the rotations around axis passing by a given point O. Combine two successive rotations, around different axis. This is not commutative. Exercise : show that, using orthogonal axis system (OX, OY, OZ), combined rotations around these axis is not a commutative operation.. Take any object.
- Make a rotation +90° around OX, then a rotation +90° around OZ
Return to initial conditions and :
- Make a rotation +90° around OZ, then a rotation +90° around OX
Compare the results.
Group's action.
...A
group G is composed by square matrixes g . They can be multiplied.
We will say that a group may act on itself .
The group may also act on a space, made of points, described by column vectors.
Example :
(24)
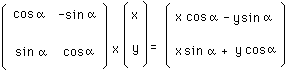
If we write :
(25)
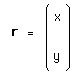
the action of the group
on this space becomes :
(26)
...In
this peculiar case the action on space identifies to the simple matrix multiplication.
But the concept of an action is much more general.
![]()