...Our starting point will be a group Dynamic G , i.e. a family of square matrixes g .

...Dynamic : because time is involved .

...This group has a certain dimension n .It may act on a space X, which has its own dimension ( which has nothing to do with the dimension of the group, this last being the number of independent parameters which define each matrix g of the set, forming the group G ).

...Now we need an action , to define a space on which the group acts, its momentum space. This space is not space-time in which the particles are supposed to travel. Building such space will take us in a strange country, which will looks like some schizophrenic land. But if you follow this way you will be closer to physical reality that you have never been before.

...When we will have a space to play with, and an action ton act on, we will classify the moments-movements into species and identify such species to elementary particles.

...Above we said that the produce of a group by a vector, corresponding to SO(2) and O(2), as well as SO(3) and O(3) corresponded to an action :

i.e :
(166b)

 
Notice we could write it in the equivalent way :
(167)

For oriented Euclid's group and complete Euclid's group we need to write an action :
(168)

But these actions, as well as the corresponding actions of dynamics groups on space, like :
(169)

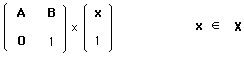
give ... nothing. They just carry objects in space, or space-time, or more refined spaces ( 5 dimensional space, ten dimensional space ).

We have to search something "hidden under the group" : itsmomentum space ( all groups of matrixes own one ) and its

which corresponds to real physics.

What is physics ?

...Good question. The French mathematician Jean-Marie Souriau invented the concept of coadjoint action of a group on its momentum space and showed, in the early seventies. In the following this will be developped.

...Of course, the physicist, at the end of the calculation, will ask

...In other terms, it works, but can we give a physical meaning to this concept of coadjoint action of a dynamic group on its space momentum. The answer seems to be no.

 
...Imagine you are a student of Aristotle. Suddently you have a intuition and you invent a new word to name it :
 

...Aristotle arrives. He has been warned by other students that you had invented something new, and he asks ;

- Could you explain to us what means inertia ?

You will be unable to do it, using Aristotle's words. You will have encouneted a paradigmatic change.

 
Jump to the middle-age. Try to explain a chemical reaction in terms of four elements vocabulary. Impossible too...

The coadjoint action of a group on its space momentum is a paradigmatic change. It is a new insight on physics.

In fact, physicists handle group actions all the time when they speak about "invariance", conservation laws".

 
Such conventional physicist will ask :

- Can you explain to me what is the meaning of the caodjoint action of a group on its momentume space, in simple worlds, if possible ?

We answer :

- Why do you use conservation laws, in physics ?

- Aoh... because there are conservative quantities : energy, mass, electric charge...

- Why are they conserved ?

- But, it is a basic principle ! ....

- My dear friend, consider the caodjoint action of a group on its momentum space as a basic principe.

- What do you mean ?

- Any physics is based on a group structure. If you identify the group, you may build its caodjoint action and the corresponding momentum space. Then the components of the moment are the corresponding physical quantities.

- ........

 
Warning. If you are a physicist (even a theoretical physicist...) and if you read what follows you will undergo a paradigmatic mutation. After, physics will be simply... different.
 

Actions.

What is an action ?
Something linked to a group, which obeys the following axioms :
(170)

Of course, for groups of matrixes, the composition operation is :

For matrixes groups we can write :
(171)

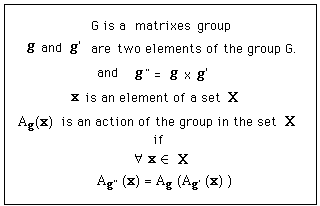
Consider the column-vector :
(172)

 
where x , for an example, represents vectors
(173)

 
Does
(174)

fits the action's axioms ? Let g and g' be two elements of the group G.
(175)

We must have :
(176)

i.e :
(177)

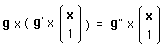
under associativity property :
(178)

is a group's action.

...Notice we put the element g of the group G on the left. What happens if we put it on the righ ? Then it must be combined to a line-matrix y.
(179)

Is it an action ?