...vWe extend the precedent group to a four-components orthochron set. This operation gives a geometrical interpretation of antimatter after Dirac.
1) Introduction :
...In a former paper [1] we have presented a description of elementary particles ins a ten-dimensional space, i.e. space-time (x,y,z,t) plus six additional dimensions :
(1)
We presented a 16-dimensions group, an extension of the
Poincaré orthochron subgroup, acting on :
- its 16-dimensions momentum space
- its 10-dimensional movement space.
The six additional components of the momentum have been identified to the charges of the particles :
(2)
so that the momentum becomes :
(3)
(4)
after J.M.Souriau [1].
We have figured the link between the species of moments and the species of movement, suggesting that :
- The movement of matter corresponds to { z i > 0 } sector.
- The movement of antimatter corresponds to { z i < 0 } sector.
- The movement of photons corresponds to { z i = 0 } plane.
All that must be now justified.
2) Introducing a four components group. Geometrization of Dirac's antimatter.
...The precedent 16-dimensional group had two components, correspondong to the two orthochron components of the Lorentz group, Ln ( neutral component ) and Ls , with :
(5)
Our group was an extension of the orthochron Poincaré sub-group :
(6)
and we wrote it :
(7)
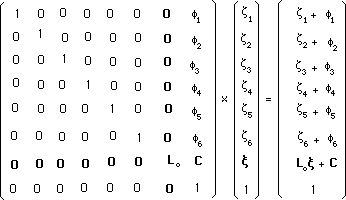
The corresponding coadjoint action was :
(8)
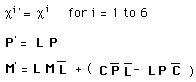
with :
(9)
...In such a group no element transforms the movement of a matter mass-point into the movement of an antimatter mass-point, and vice versa. According to the chosen definition of antimatter, through a :
(10)
some element should reverse the additional dimensions. With :
(11)
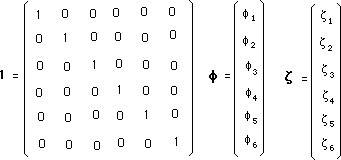
we can write the precedent group into a more compact form
:
(12)
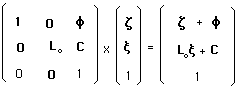
It contains the neutral element :
(13)
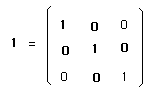
The matrix that reverses the additional dimensions is be the following orthochron commuter :
(14)
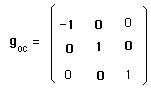
We can duplicate the precedent group through the operation
:
(15)
It is equivalent to write the new four component group, whose element is :
(16)
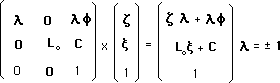
The corresponding coadjoint action is :
(17)
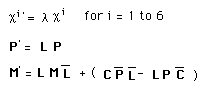
We see that ( l = - 1 ) reverses the charges. In that case the inversion of the additional dimensions :
(18)
goes with a :
(19)
which corresponds to Dirac's description of antimatter
[4], so that the present paper represents a geometrization of antimatter after
Dirac.
