7) Gravitational lensing due to negative mass matter.

...In classical general relativity the (steady) geometry of space-time, in and around a sphere filled by constant density matter, and surrounded by void is described by two joined metrics. The first is the "internal Schwarzschild metric" :

with the condition :

and the second the "external Schwarzschild metric":

...Classical gravitational lensing is computed with the second, where m, a simple integration constant, is chosen positive. Then the plane trajectory of a massive particle is given by

where phi is the polar angle, and u the inverse of radial distance r, with respect to the geometric centre of the system. The photons obey :

where c is the light velocity, h and l paths parameters. This gives the classical schema of figure 10-a where the central mass is reduced to a simple mass-point. Now, have a look to (16) and (18). We can change the sign of the mass density and R _s into – R _s. Then we get the :
(16bis)

...These solution can be linked and describe the geometry in and out a sphere filled by negative mass. The first is solution of the field equation

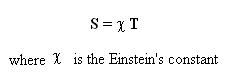
The second comes from S = 0 . As introduced in 1995 in reference [3] we get a negative lensing effect. See figure 10-b

Fig. 10-a : Positive gravitational Fig.10-b : Negative gravitational
lensing effect lensing effect

...Notice we may now use the internal solution for photons can cross a negative mass clump, according to our assumption (like neutrinos can cross the sun. But we have no telescopes using neutrinos). Now, examine the impact on observations. The first one is the reduction of the luminosity of large redshift galaxies, by negative gravitational lensing effect due to twin matter clumps. As the matterfact, we find many faint galaxies at large distance. The classical interpretation consists to say that dwarfs galaxies form first, then merge to give heavier objetcs. Negative lensing provides an alternative explanation. Now, let us show that negative lensing, due to surrounding twin matter, can explain observed strong lensing effects, around galaxies and clusters of galaxies. First, notice than any homogeneous distribution of matter, with positive or negative density, does not induce gravitational lensing. Only non-homogeneous distribution dot it. Let us figure schematically a galaxy imbedded in some sort of hole in an homogeneous twin matter distribution. See fig. 11-a.

Fig. 11 : Combination of positive (due to the confined object) and negative (due to the surrounding twin matter) lensing effects. Reinforcement of the global effect.

... We have schematised the reinforcement of the gravitational effect due to twin matter surrounding a spheroidal mass M ( spheroidal galaxy or spheroidal cluster of galaxies). As shown in section 18 the gravitational field due to a spheroidal hole in a constant density negative mass distribution is equivalent to the field due to a constant density sphere, filled by positive mass (figure 11-b). On figure 11-c we have figured the contribution of the positive mass M to the gravitational lensing effect. The main effect (figure 11-c) is due to the hole, which focuses the light rays. On figure 11-a we find the two effects, combined. As a conclusion the observation of strong gravitational lensing effects at the vicinity of galaxies or clusters of galaxies is not the final proof that some positive mass invisible dark matter is present. There is an alternative interpretation : the object could be surrounded by negative matter, which focusses the light rays.

8) Exotic matter or exotic geometry ?

...As said above, physicists have difficulty to stand the idea that negative mass could exist in our universe. By the way, the classical standard model does not bring all the answers. For example, nobody knows where the primeval antimatter is gone, so that half part of the universe is missing. The question became so embarrassing that today scientists just choose to avoid it. In 1967 A.Sakharov suggested that some "twin universe" would have been created during the so-called Big Bang, where the arrow of time could be reversed ([33],[34],[35]&[36]) . The idea of a couple of universes interacting only through gravitational force is in progress, see a recent paper of Nima-Arkani Ahmed (Dept. of Phys. of Berkeley U.), Savas Domopoulos (Dept. of Phys of Stanford U.) and Georgi Dvali (Dept. of Phys. Of new-York Univ.), reference [43] and references [37] to [42] .
...Assume the universe is the two-folds cover of a M4 manifold.

Fig.12 : Two folds cover of a manifold.

...We get a point-to-point mapping, linking two "conjugated points" M and M , which can be described by a same system of coordinates

We can give this non simply connected two-folds cover a metric structure (similar to the two-points bundle of a manifold M4). We can give a manifold any number of distinct metrics. Each defines a metric space. The underlying manifold gives a point-to-point mapping, linking all the points of these metric spaces. We get two coupled metric spaces F and F.

Here we take two riemanian metrics with the same hyperbolic signature (+ - - - ). We call the metrics g and g . From these two metrics we can build geodesics systems but, as F and F and disconnected, the two families of geodesics are disconnected. As a conclusion, if these metrics give null-geodesics and if one assume that light travels along them in both folds, any structure of a given fold will be geometrically invisible from the other one. In classical General Relativity one considers a single fold, associated to the field equation (Einstein equation)

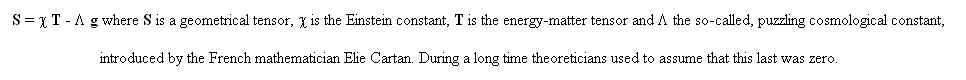
Then, non-steady solutions, corresponding to homogeneous and isotropic conditions give the Friedman models. Steady-state solutions, while spherical symmetry gives the internal Schwarzschild solution (16), from the equation

where T is a constant tensor field, inside a sphere whose radius is r_o.

The external Schwarzschild solution (18) comes from S = 0 with spherical symmetry too. The choice of a field equation is an a priori choice. If metric solutions are asymptotically flat, Lorentzian, it ensures the validity of Special relativity in vacuum. If one makes an expansion into a series around a Lorentz metric, in steady state conditions, the field equation can be identified to Poisson equation

In addition, the Newtonian approximation provides the Newton law of interaction. Friedman models, corresponding to solutions of the field equation, provide a redshift, which is observed. Locally, the bending of light rays at the vicinity of the sun as well as the precession of Mercury's perihelion are observed too. But recently some discrepancy between Friedman models and Hubble's constant measurements lead today the cosmologists to reintroduce a non-zero cosmological constant, corresponding to some mysterious "repulsive power of vacuum".
...Now, return to the two-folds structure. Introduce two tensor fields T and T which are supposed to describe the contents of folds F and F. From metrics g a

nd g we can define derive geometric tensors S and S. We can link the four tensors S , S , T , T into a system of two coupled field equations, inspired by Einstein equation

9) First geometrical interpretation of the dark matter phenomenon.

Consider the following coupled field equations:

...Basically, they are identical, so that g identifies to g : the image of a geodesic of fold F becomes a geodesic of fold F. We get two "parallel" universes, which interact only through gravitational force. Dark matter can be composed by atoms, neutrons, protons, photons, identical to ours, except we cannot observe twin matter on geometrical grounds. If we study the Newtonian approximation, we get the following Poisson equation :

...In this model :

- matter attracts matter
- twin matter attracts twin matter
- matter and twin matter attract each other.

...But this does not solve all the observational data : even if some geometrically invisible dark matter would lie in the adjacent portion of our universe, near by the Abell 1942 cluster, this does not explain why this attractive force field would not capture our own galaxies and gas, lying in our fold of the universe. That's for we deal with the following set of equations (reference [3] and [4] ) :

10) Second geometrical interpretation of the dark matter phenomenon.

...Consider the following coupled field equations system :

Notice this definitively not imply g = - g . The Newtonian approximation supports the assumptions of section 3. We get the following Poisson equation :

...We prefer to consider that the twin universe, the twin fold, is filled by intrinsically positive mass matter and that the minus sign in the field equation gives it the appearance of a negative mass for an observer located in our fold. Then we may call it "apparent mass". The symmetry of system (29) plus (30) makes the definition of positive and negative energies purely arbitrary. What about the classical local check of the RG ? In this new model :

- matter attracts matter, through Newton law.
- twin matter attracts twin matter through Newton law.
- matter and twin matter repel each other through an "anti-Newton law".

...The solar system is a very dense portion of the universe. In the adjacent portion of the twin fold, twin matter is pushed away. Then the system is very close to :

...The first equation identifies to Einstein equation, so that all the classical verifications fit. . What about gravitons ? Which path do they follow ? The answer is composed by two arguments :

- Field equations provide macroscopic description of the universe, which ignores the existence of particles and just gives geodesic systems.

- By the way : what's a graviton ?

Notice that recently  [49], anomalous long-range (negative) acceleration has been evidenced for space probes Pioneer 10 and Pioneer 11, at long distance from the sun (40-60 AU). An unmodelled acceleration, directed towards the Sun, (8.09 ± 0.20 ) x 10^-8 cm/s² for Pioneer 10 and (8.56 ± 0.15) x 10^-8 cm/s² for Pioneer 11, was evidenced and described as a not-understood viscous drag force. Similarly, and unmodelled acceleration towards the sun was found for the probe Ulysse (12 ± 3 ) x 10^-8 cm/s². See complete discussion in this interesting paper. The authors say : The paradigm is obvious : s is it dark matter or modification of gravity ”. As the pointed out, if dark matter is called for explanation, it would correspond to a total dark matter amount > 3 x 10^-4 solar mass, which would be in conflict with the accuracy of the ephemeris. A 3d neutrino model also did not solve the problem [50]. Others try to modify the Newton law, adding a Yukawa force  [51]. But “this anomalous acceleration is too large to have gone undetected in planetary orbits, particularly for Earth and Mars”. Then they focus on available Viking probes data and conclude : “But a large error would cause inconsistency with the overall planetary ephemeris…. if the anomalous radial acceleration acting on spinning spacecraft is gravitational in origin, it is not universal. That is, it must affect bodies in the 1000 kg range more that bodies of planetary size by a factor 100 or more (…), which would be a strange violation of the equivalence principle”. An alternative interpretation of this still puzzling phenomenon would be the action of weak repulsive twin matter distribution between stars, inside galaxies, which would form, as for spiral structure, a weak potential barrier. To be investigated.

11) The question of the repulsive power of vacuum. An alternative answer.

...When we look to equation (29) we see that T acts like a "cosmological constant". It figures the "repulsive power of the twin universe", which can play a role in non-steady coupled solutions. Assumption of homogeneity and isotropy gives the Riemanian metrics the well-known Robertson-Walker form, as follows :

...The radial distances between conjugated points (same u, an non-dimensional "radial distance", with respect to an arbitrary point) are not automatically equal :

r = R u .......................r = R u

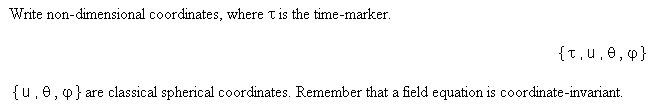
The choice of coordinates remains free, in each fold, where we can define different cosmic times :

. t ...et ... t

R = cT R R = c T R

...We put the field equations into their non-dimensional forms, using :

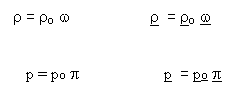
Following, these tensors, written in their non-dimensional forms :

At the end, we get four second order coupled differential equations (instead two, in the classical approach). :

...We need some additional hypothesis. Assume that the two universes have "parallel lives" during their radiative epoch, i.e :

which impose negative curvature indexes ( k = k = -1 ). After decoupling we neglect the pressure terms (dust universes) :

from which we get immediately :

Introducing the mass-conservation in both folds :

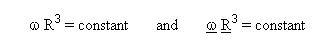
the system becomes :

...Notice that R = R gives R" = R" = 0. On another hand, if the two universes were "fully coupled", i.e. R/R = constant, this peculiar solution would correspond to Friedmann models, with "parallel evolutions". But we consider that they are coupled by gravitational field, through (54-a) and (54-b), which shows that the linear expansion is unstable. If, for an example, if R > R then R" > 0 and R" < 0 . The system can be numerically solved. The typical solution corresponds to figure 13. The numerical values have been chosen in order to fit the initial condition for VLS numerical simulation. The law of evolution, for the radiative epoch will be justified in section 15.

Fig.13 : The evolution of the scale parameters  of the universe and twin universe.

...We see that this system of two universes interacting through gravitational force is unstable. If one universe goes faster, pushed by his twin, the other one slows down. The observed acceleration of our universe is then caused bay the "repulsive power of its twin universe". The histories of the two differ. Ours is cooler and more rarefied. The twin is warmer and denser. This justifies the assumption of section 2, which determines the VLS.
...What could be the evolution of our twin universe ? As we have seen, it is filled by huge clumps of twin matter which look like huge proto-stars, whose cooling time is fairly larger than the age of the universe. Fusion does not occur in the twin universe. We think after first nucleo-synthesis, it remains filled by hydrogen and helium. Life phenomenon would not exist in the twin universe.

12) Newton’s law and Poisson equation.

In classical General Relativity the Newton law and the Poisson equation can be derived from Einstein field equation, considering an almost steady state and almost Lorentzian metric solution. Here, we have two perturbed metrics, written in non-dimensional coordinates h(time) , z ^a (space)

Expanding the two field equations into series, and considering an almost uniform universe we get

Introduce a non-dimensional gravitational potential :

Defining a non-dimensional Laplacian operator :

we get a non-dimensional Poisson equation :

The classical method of identification gives the Newton law. In fold F :

In fold F :

The gravitational potential acts differently on a (m = +1 ) test-particle. Depends the fold it belongs to. In general a (m= +1) particle located in fold F gives the following contribution the the (non-dimensional) gravitational potential.

As we can see, the system of coupled field equations determines completely the dynamics of the system, corresponding to Newtonian approximation, as introduced as an hypothesis in the beginning of the paper. In the model the velocities of light c and c may be different (and we think they are). Using the dimensional quantities introduced in section 11 we may return to dimensional laws, as following :

The Newton law, expressed in the two folds, becomes :

The Poisson equation can be expressed indifferently in both folds

13) Scalar curvatures.

What is the geometrical meaning of the system (29) plus (30) ? The scalar curvatures R and R are opposite. We may give a didactic image of this new geometrical framework. First, remember that the structure corresponds to a two-folds cover of a manifold. We get two distinct folds, with coupled metrics g and g. They are note independent, for they are solution of the field equation system. They produce their own system of geodesics and the image, in fold F, of a geodesic of fold F is not a geodesic of that twin fold F. Light follows null-geodesics in both folds, but no null-geodesic links the two, so that the structure of one fold are geometrically invisible for an observer located in the other one. Assume now a mass is present un fold F, while the adjacent portion of fold F is empty. The corresponding field equations system would be :

Assume this mass distribution corresponds to a sphere with radius r_o, filled by constant density material, and surrounded by void. Then the geometry, in fold F, is steady state is assumed, corresponds to two linked Schwarzschild solutions (internal and external). They are solutions of equation (68). In fold F we get a conjugated geometry, with opposite scalar curvature R = - R. Outside the sphere (and outside the corresponding adjacent space in fold F) R = R = 0. Inside the scalar curvatures are constant. The didactic model corresponds to a blunt “posicone”, associated to a “blunt negacone”, as shown on figure 15. In a blunt “posicone” the central portion is a portion of a sphere.

Fig.14 : A mass is present in the fold F. Induced negative curvature in fold F

In un “blunt negacone” the associated region corresponds, in this 2d didactic image, to a horse saddle. Below, a plane which figures how an observer located in fold F conceives this. He can observe both the mass M (grey disk) and the path of a mass cruising in his fold, “attracted by this mass” , this path, in this Euclidean representation corresponding to the projection of a geodesic of the “blunt posicone”. The observer cannot see the path of a particle of “twin matter”, cruising in the twin fold F and repelled by the mass.

Now, assume the mass is located in the fold F, in the twin space. The situations are reversed. See on figure 15. Following this 2d didactic image, the fold F is shaped as a blunt negacone, while the fold F looks like a blunt posicone.The geometry of F, close to the geometrical centre of the system evokes the vicinity of a twin matter clump located at the centre of a “cell” in the VLS. Light travelling in our fold can cross it, but it is sprayed. As evoked in section 3 and on figure 7 it implies that the clumps’ diameters could not be larger than a certain value, to be computed, in order to fit the available observations. Below : two plane representations showing Euclidean projections (how an observer could conceive the phenomenon, when located in fold F or in fold F).

Fig.15 : A mass of “twin matter” is present in the fold F, while the fold F is empty.
It produces a negative (induced) curvature in F.

---

Paper's Summary