(247)

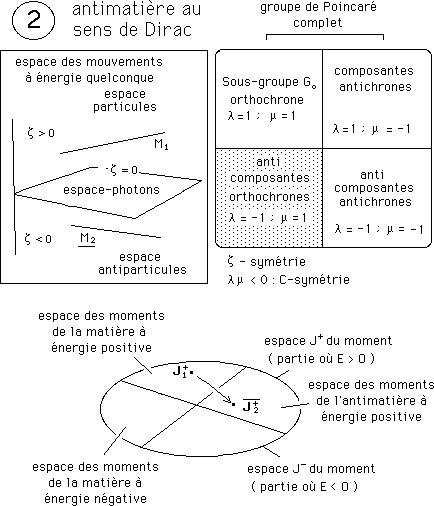
On a une z-symétrie. Donc notre matière est transformée en antimatière, selon la définition que nous avons donnée plus haut. L'action coadjointe donne C --- - C . Il y a conjugaison de charge. Masse et énergie sont inchangées. Il s'agit de l'antimatière au sens de Dirac, orthochrone. Les charges sont inversées, à commencer par la charge électrique q.

Passons au secteur ( l = -1 ; m = -1 )

(248)

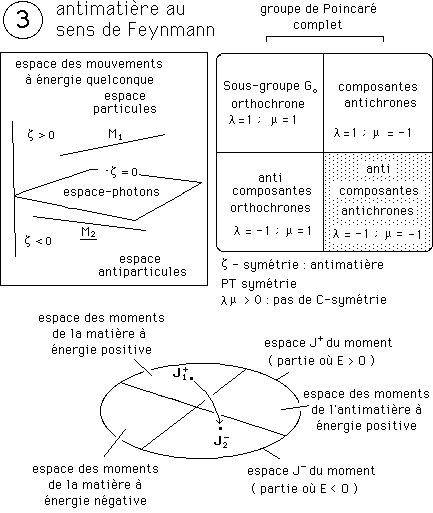
On a une z-symétrie, donc transformation de la matière en antimatière. Comme lm est positif, il n'y a pas de C-symétrie. Les charges sont inchangées. Il y a par contre PT-symétrie. C'est ce qui a fait dire à Feynmann que de la matière ordinaire ( avec les mêmes charges ), énantiomorphe et remontant le temps se comporterait comme de l'antimatière au sens de Dirac (laquelle est C-symétrique). Mais c'est oublier une chose. L'antimatière de Feynmann est "antichrone", donc possède une masse et une énergie négative. Dans un champ de pesanteur, elle devrait "monter".
 

Notre conclusion :

 Il n'y a pas équivalence entre ces deux antimatières.

Passons au dernier type de mouvements, induits par les éléments de ( l = 1 ; m = -1 ). Il n'y a pas z-symétrie. Ce mouvement est donc celui d'une particule de matière. Il y a PT-symétrie, du fait que m = -1.

L'action coadjointe, du fait que lm < 0 donne une C-symétrie. L'objet est donc CPT-symétrique.

The "théorème CPT" identifie la CPT-symétrique d'une particule avec cette particule elle-même. Mais nous pensons que ça n'est pas vrai. Ces CPT-symétriques particules sont engendrées par des éléments du groupe qui appartiennent à un secteur antichrone. Donc les masses et les énergies des CPT-symétriques sont négatives.
Il n'y a pas équivalence entre les deux types de matière.
 

(249)
 

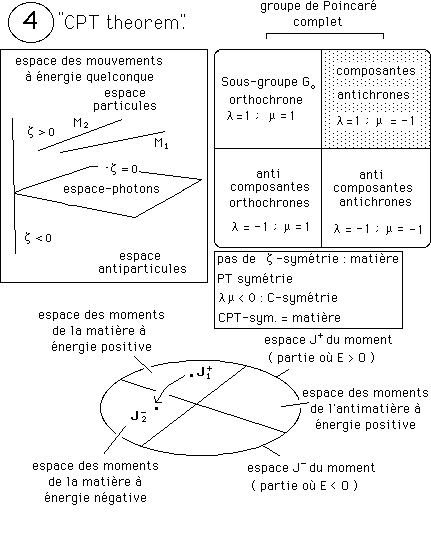
Au passage, des précisions sur les mouvements des photons. Les anticomposantes orthochrones ont, sur les mouvements des photons, une action coadjointe correspondant au schéma 1 BIS. (246, page précédente)

Par contre, si on fait agit des éléments appartenant aux secteurs antichrones ceci aura pour effet d'inverser l'énergie de ces photons. Schéma 4 bis, ci-après :

(250)

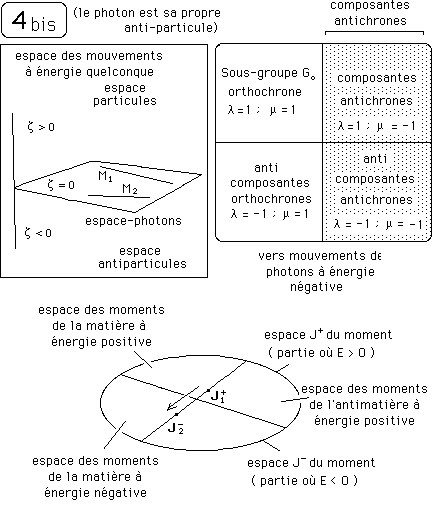
Mais dans cette optique on reste avec des particules, qu'elles aient des masses non-nulles ou nulles, dotées d'énergies opposées, qui peuvent se rencontrer. En effet on sait que tout ce qui est antichrone va avec E < 0 et m < 0 .

Selon ce modèle, correspondant au 1° - groupe de Petit, en résumé :

- Un seul univers, dont le groupe dynamique est :

(251)

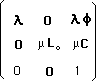
à huit composantes, agissant sur un espace décadimensionnel (l'espace-temps plus six dimensions additionnelles).

- On a différentes symétries. La z-symétrie ( l = - 1 ), affectant toutes les dimensions additionnelles, est prise comme définition de la dualité matière-antimatière. La PT-symétrie ( m = - 1 ).

- Le groupe contient des composantes orthochrones et des composantes antichrones, associées à des mouvements à énergie et masse négatives.

- L'analyse de l'action coadjointe permet de mettre en évidence la C-symétrie ( inversion de toutes les charges ), conditionnée par la z-symétrie et la PT-symétrie C = l m

- On a quatre types fondamentaux de mouvements, donc de matières.