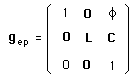
..When Souriau explicits the action of the different elements of the Poincaré group, he finds :
gp ( Ln , C) : I E --> E ; p --> p ; f ---> f ; l ----> l
..The elements of this orthochrone (neutral) component of the group conserves energy, momentum, passage and spin
gp ( Ls , C) : I E --> E ; p --> - p ; f ---> - f ; l ----> l
..This element of the second component of the orthochron subset of matrixes of the Poincaré's group conserves energy and spin, but reverses passage and impulsion.
gp ( Lt , C) : I E --> - E ; p --> p ; f ---> - f ; l ----> l
..This element of the third component of the group, which belongs to the antichrone subset (after Souriau's definition) reverses energy and passage, but conserves impulsion and spin.
gp ( Lst , C) : I E --> - E ; p --> - p ; f ---> f ; l ----> l
..This fourth, which belongs to the antichron subset of the Poincaré's group conserves passage and spin, by reverses energy and impulsion.
In the four cases, the spin is unchanged.
The element of the two antichron components of the Poincaré's group reverses energy
..This is a very important results, found by Souriau in 1972, which can be found in his book, chapter III, page 197 (in french edition), devoted to inversions of space and time.
Quantum features come from the so-called "extended Poincaré group" :
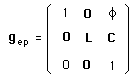
....Then the dimension of the group becomes 11.
....f is a phase.
...A group acts on its associated space (here space time plus additional dimension z , "Kaluza dimension"). But it acts on its momentum space, through coadjoint action. The number of the components of the moment J is the same than the number of dimensions of the group. For the non-extended poincaré group, the components of the moment are :
....Classically, these components a grouped :
Jep = { c, M , P } = { c, M , p , E}
where p is the impulsion :
p = { px ,py , pz }
while E is the energy. P is the four-vector :
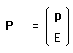
M is an antisymmetric matrix, as defined by Souriau :
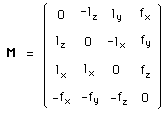
....If we consider the extended Poincaré group, we get an extra scalar component to the moment, classically identified to the electric charge :
....The action of the extended Poincaré's group on its momentum space gives :
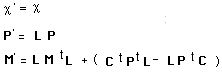
....That we "read" : conservation of the electric charge c . It is now possible to extend this group, adding new extra-dimension, similar to Kaluza's one. In the following Lo represents the orthochron subgroup of Poincaré's group. Notice that :
- Lo gives the antichron subset for :
- Ln = Lst
- Ls = Lt
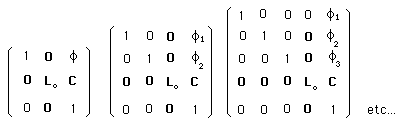
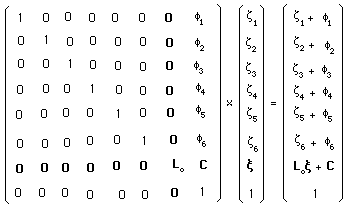
....Here, we have limited the Lorentz group to its neutral component Lo, which be explained later. The subsequent action of this extended group on its momentum space becomes :
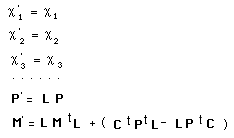
....The first lines only shows the conservation
of quantum number, que electric charge being one of them.
Geometric definition of Dirac's antimatter.
....Introduce the following vector f and matrix l :
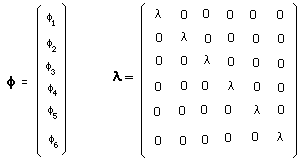
....Now, introduce the new group :
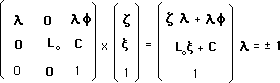
....It is a two component group. Clearly, from above, the l = -1 component reverse the quantum charges ci . Notice that it reverses the zi dimensions too. We suggest this is the general geometric definition of antimatter is a ( z - symmetry ) : inversion of the extra-dimensionszi .
Geometric definition of Feynman antimatter.
Now write the group :
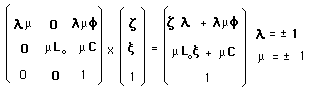
....It becomes a four components group. ( m = 1 ) elements achieve PT-symmetry. The corresponding action on the momentum space becomes :
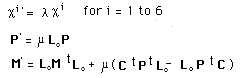
....Take ( l = + 1 ) and ( m = -1 ). We get a PT-symmetry. Quantum charges are unchanged, but extra-dimensions are reversed. According to our geometric definition of antimatter, this corresponds to Feynman's antimatter.
Group acting on a two-points bundle space.
..Introduce a bundle indix b and write a new groups'action :
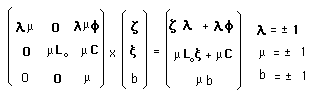
..The action on the momentum space is identical. A dynamical group runs mass-points movements. Given a movement, an element of the group may define another one and we have seen that antimatter was nothing but a different movement of the particle, along reversed additional dimensions zi . The Poincaré's group aroses a physical problem, introducing antichron movements, corresponding to T-symmetry. Similarly, the so-called Feynmann's antimatter aroses the same problem, for the considered movement was T-symmetric too. Here, the problem is solved, for antochron movements take place in the twin space, in the b = -1 fold of the bundle.
m = 1 causes a T-symmetry and what we will call a B-symmetry (bundle symmetry).
..Now, positive energy and negative energy particles cannot encounter and fully annihilate for the "live" in distinct twin folds.
Geometric interpretation of the CPT theorem.
..In the above group, choose :
l = -1 ; m = -1
..We achieve a CPT-symmetry :
- space-time is reversed
- quantum numbers ci are reversed
but additional dimensions zi are unchanged, so that this corresponds to a partcle of matter. The CPT-symmetric of a particle of matter is a particle of matter, except it owns negative mass and energy and live in the twin fold.
CTP-symmetric of matter in the matter of the twin fold, whose contribution to the gravitational field is negative.
..Similarly, if we choose :
l = +1 ; m = -1
we get the PT-symmetrical of the particle. If we take a particle of matter, its PT-symmetrica is antimatter, for we have a z-symmetry. It lives in the twin fold, due to the subsequent B-symmtry.
Matter-antimatter duality holds in the twin universe.
..All particles of the twin universe have apparent negative energy (including photons, neutrinos, and so on). All massive particles own an apparent negative mass. Quod erat demonstrandum.
References :
[1] A.Sakharov : "CP violation and baryonic asymmetry of
the Universe". ZhETF Pis'ma 5 : 32-35 (1967) : Traduction JETP Lett.
5 : 24-27 (1967)
[2] A.Sakharov : "A multisheet Cosmological Model" Preprint Institute
of Applied Mathematics, Moscow 1970
[3] A.Sakharov : "Cosmological Model of the Universe with a time-vector
inversion". ZhETF 79 : 689-693 (1980) : Traduction in Sov. Phys.
JETP 52 : 349-351 (1980)
[4] A.Sakharov : "Topological structure of elementary particles and CPT
asymmetry" in "problems in theoretical physics", dedicated to
the memory of I.E.Tamm, Nauka, Moscow 1972 pp. 243-247
[5]J.P.Petit : "Univers
énantiomorphes à flèches du temps opposés", CRAS
du 8 mai 1977, t.285 pp. 1217-1221
[6]J.P.Petit : "Univers en interaction avec leur image dans le miroir du temps".
CRAS du 6 juin 1977, t. 284, série A, pp. 1413-1416
[7]
J.P.Petit : The
missing mass effect. Il Nuovo Cimento, B , vol. 109, july 1994, pp. 697-710
[8] J.P.Petit,
Twin Universe Cosmology. Astrophysics
and Space Science. Astr. And Sp. Sc. 226 : 273-307, 1995
[9] J.P.Petit,
"On a perdu la moitié de l'univers", Ed. Albin Michel, France,
1997.
[10]
- J.P.Petit : An
interpretation of cosmological model with variable light velocity. Modern
Physics Letters A, Vol. 3, n°16, nov 1988, p.1527
[11]
- J.P.Petit : Cosmological
model with variable light velocity: the interpretation of red shifts.
Modern Physics Letters A, Vol.3 , n° 18, dec. 1988, p.1733
[12] -
J.P.Petit & Maurice Viton : Gauge
cosmological model with variable light velocity. Comparizon with QSO
observational data. Modern Physics Letters A Vol.4 , n°23 (1989) pp. 2201-2210
[13] -
R.Adler, M.Bazin and M.Schiffer : Introduction to general relativity, Mc Graw
Hill Book Cie. 1975, chapter 14, "TOV equation".
[14] -
Oppenheimer J.R. and H. Snyder (1939) : On continued gravitational contraction,
Phys. Rev. 55 : 455
[15] J.M.Souriau : Structure
des Systèmes Dynamiques, Dunod-France Ed. 1972 and Birkhauser Ed. 1997.
[16] Interview of Fort,
Ciel et Espace Jr. June 2000.
![]()