| sciences | jp-petit.com |
Presentation
of the article
Questionable
black hole
French translation :
Des doutes sur l'existence des trous noirs.
Authors :
Jean-Pierre Petit, Marseille Observatory
| sciences | jp-petit.com |
Pierre Midy, Orsay CRI.
To go straight to the scientific paper.
This
work represents the results of ten years of effort. For the last 30 years, astrophysicians
have had only one term on their lips "black holes". The subject fascinates
the public and several books have already been devoted to it. However observational
confirmation is still lacking : black holes "shine by their absence".
And yet the cosmos is vast. Our galaxy alone contains at least 100 to 200 milliard
stars.
The
existence of certain objects has been shown by observation, quasars for example.
We now know of more than four thousand of them. That does not mean that we understand
these objects completely, how they are formed, how they evolve and their lifespan.
In fact we do not know anything about them. They are just catalogued in the
same way as were "nebulae" in the astronomer Messier's time.
Apparently certain quasars live in the centre of formations of the type galaxy.
These galaxies have an "active core", which could mean anything and
nothing at the same time we know nothing of the nature of the activity, what
its energy source is for example.
Contemporary astrophysics seems to satisfy itself with little. To the question
:
- What is a quasar ?
The astrophysician replies :
- It is the core of an active galaxy.
And to the question :
- What is an active galaxy ?
He will reply :
- It is a galaxy with a quasar at its center...
Recently, a few years ago, we discovered "gamma flashes", one per day. The cover of the French magazine Ciel et Espace (Sky and Space) once had the headline "gamma flashes : a mystery solved at last". Reply, in the magazine's columns : a small, brilliant spot has just been observed at the position of a detected gamma flash. Meaning : solving a mystery means knowing that areas of the sky that emit flashes also emit light....
Isn't that a little .. poor ?
Conversely, other objects exist whose existence was surmised, often with good precision, before their observation. The typical example is the supernova, described in 1931 by the American astrophysician (of Swiss origin) Fritz Zwicky during a famous conference at Caltech, USA. Zwicky explained at the time that sufficiently massive stars, say with masses above twenty solar masses, should come to a paroxystic end with an increase in power in the space of a few days, the whole phenomenon taking place over twenty days or so. It was a remarkable prediction, though it wasn't taken seriously at the time. However Zwicky, tenacious, discovered the first supernovae. Nowadays we know of several hundred. The same goes for neutron stars, identified subsequently with pulsars (rotating neutron stars) and white dwarves. This species too has several hundred identified individuals.
The black hole was proposed as an answer to a problem : what becomes of a neutron star that exceeds a certain "critical mass". These neutron stars, clearly identified, resemble enormous nuclei of atoms, without protons. Why are these objects composed exclusively of neutrons?
We consider neutron stars to be what remains of the iron core of a massive star after it has exploded. A massive star is a star in which several types of fusion take place during its lifetime. It ends by producing iron which cannot take part in any further exo-energetic fusion reaction. This iron, heavy, falls to the centre of the star therefore, like ash in a fireplace. When the star suddenly runs out of fuel (as Zwicky understood) it collapses on itself à 80,000 kilometres per second (give or take a kilometre per second of course). When falling onto the iron nucleus this gaz is strongly compressed. Not only does it bounce off, but several fusion reactions are produced and which no longer need to be exo-energetic as energy comes from the brutal contraction of the star on itself. All sorts of nuclear species are created, including many radioactive atoms of extremely variable lifetimes. In 1987 the explosion of the star Sanduleak, in the Magellan cloud, gave definite confirmation of the existence of such phenomena (only 150,000 light years away).
The
phenomenon crushes the iron core completely by dislocating its atoms. It becomes
so compressed on itself that electrons no longer have sufficient space to move
between nucleons. Trapped, they therefore combine with protons to give neutrons
and neutrinos.
Normally, when we compress a gas, the phenomenon known as pressure counteracts
the compression. This is also true for a liquid or a solid (everything is compressible).
This is what happens when a young star is born. The proto-star is a mass of
gas which settles on itself. But in doing so it heats up and the force of pressure
limits contraction. It is a poor radiator but must lose energy by radiation
(infrared) before it can contract enough to become a real star. However if its
mass is insufficient it will become a "big Jupiter" (this giant planet
continues to radiate more energy than it receives from the Sun but will never
become a star).
When the explosion of a supernova compresses the iron nucleus, the latter evacuates
its energy by emitting a fantastic quantity of...neutrinos. Here the scenario
changes completely : radiative cooling is instantaneous because the neutrinos
can escape without difficulty. No counter-pressure therefore. The lump of iron
is crushed lamentably. Just a pile of neutrons remains, pressed up against each
other like Japanese in the subway during rush-hour.
Why a critical mass? Because the neutrons cannot take a pressure greater than
a maximum value. Like electric lightbulbs piled up in a mineshaft. After a certain
level of bulbs the glass will break and a pile of broken glass will fall to
the bottom of the shaft.
When a neutron star has a mass a little greater than twice the mass of the Sun,
pressure in its core becomes too great. The neutrons can no longer support it.
It is then supposed to collapse on itself and no known physical phenomenon is
able to go against this "gravitational collapse". A distressing perspective
for an astrophysician.
Even before it explodes a neutron star is a "relativist", as opposed
to a "newtonian" object. This is shown by the aspect of the trajectories
of the "reference-particles" near a mass m (an atom, for example).
We know that the space-time curve phenomenon brings about a precession of the
elliptical orbit of Mercury. But the precession is minute. However, the following
figure, developed from computer calculations, shows the important precession
of a quasi-elliptic trajectory around a neutron star.
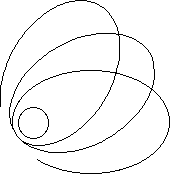
So, there is no question of describing a neutron star with "newtonian material".
The calculation programme is relatively simple and one day, when I have the time, I'll put it on the site so that you can play with it, and show the gravitational lens phenomenon (very exaggerated in the following) :
So, as it is a question of describing the destiny of a neutron star reaching criticity, a "field equation" needs to be used, that of Einstein.
S = c T
T
is a "tensor" which describes the local content in "matter energy".
The tensor is nil on the exterior and non nil on the interior. The geometric
solution must therefore be deduced from two equations.
For the interior :
S = c T
for the interior
S = 0
Solutions for this type of equation are called "metrics". However it doesn't matter what form the objects take. As well as that they are "tensors", and to understand what a tensor is, good luck ... It took me quite a while.
The Sun is associated with a local "geometry", which is the solution for the two equations. The first describes the interior of the Sun and the second the void around it. However we can only describe a sort of "ideal sun" which consists of a sphere filled with matter of constant density. But that's better than nothing. These solutions have mathematical expressions which we won't go into here. They will not mean anything to you. Each has its own "personal pathology". Let us call rn the star's radius, of constant density r. From this density r, and the value c of the speed of light, we can calculate a first characteristic radius, "R circumflex" :
![]()
The interior geometric solution is "non-pathological" if, and only if, the value of radius rn is inferior to this critical value.
With the same data we can calculate the second characteristic radius :
![]()
which we call the "Schwarzschild radius" Rs. The exterior solution, which makes reference to the "void" surrounding our star of constant density r and constant radius will be non-pathological if, and only if, the value of the star's radius rn is superior to this characteristic length.When grouping both it is necessary that :
![]()
The quantity to the right depends on the star's density (between 1015 and 1016 grammes per cubic centimetre). At constant density the quantity to the left increases as the cube of the radius Rn of the star.
This is valid for the sun, considered to be a star of constant density at first approximation. What do we mean by "pathologies"? Everything : quantities below radicals that become negative, denominators that become nil. We can see therefore that a star of constant density cannot be described by the following type of stationary solution :
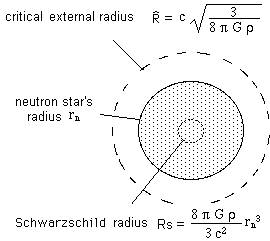
The "Schwarzschild radius" of the sun is 3,7 km : well inside (rn ). You can enjoy yourselves calculating it, given that its radius is 695,000 km, the value of the second critical radius "R circumflex" is higher.
If it was a question of the sun, on the scale of the figure the Schwarzschild radius (3,7 km) would be just a point and radius "R circumflex" would go way off the sheet. The above figure refers more to a "subcritical neutron star".
How does the "climb to criticity" take place? It suffices to add layers of neutrons, increasing in constant density (we liken the neutron star to, if not a solid, at least a drop of practically incompressible fluid).
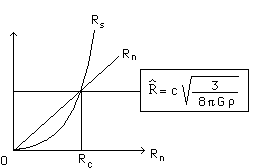
We obtain the above curves simply by using the formula shown. The star's radius increases but the "Schwarzschild radius" catches it up. And the two meet when rn reaches the value "R circumflex". Then, on the star's surface, the quantity of sub-radicals becomes negative, denominators become nil etc. This if the mathematical, geometrical translation of criticity. Which simply means that it is impossible to describe the star using either or both the combined geometrical solutions obtained from the Einstein equation with the second member non nil (interior) or nil (exterior). The characteristic maximum value of this radius is about 20 kilometres. The neutron star's density can be calculated from this.
But there is something that is little known, including among "cosmic men", even though it comes from work done during the 40's : there is another criticity, of physical nature this time, which appears just before the star's radius reaches this value. It is an extremely close value being inferior by just 5%. But when the star's radius reaches it or, which comes down to the same thing, the mass reaches a value double that of the sun's mass, pressure at the centre of the star becomes infinite , by virtue of a "TOV"model developed in the 40's by Tolman, Oppenheimer et Volkov (the Oppenheimer of the bomb).
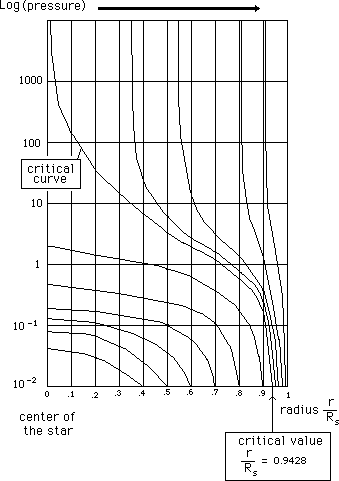
Pressure
inside a neutron star according to the distance from the centre
for different
values of object mass.
This is fundamental piece of data for us.
Hereafter the evolution of the presure, inside the neutron stard, versus the distanceto its center, for different masses :
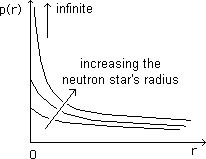
...Maybe scientists, like others, do not ask themselves questions to which they think they cannot give a reply. How does one reply to the question :
- What happens in a milieu where, at a certain point, pressure suddenly becomes infinite?
But nobody asked the question, at least not in that way. Apparently it caught nobody's eye. Many cosmology specialists with whom I have spoken were unaware of this aspect.
Let us return to "the story of the black hole". We could say : The implosion phenomenon of a destabilised neutron star is an unstationary phenomenon. Let us build therefore an unstationary solution for the ensemble of the two equations above. However we do not know how to, in a credible manner. So theoreticians turned towards the "exterior solution" (that which describes, for example, the geometry at the exterior of the sun and which becomes "pathological" at the Schwarzschild radius of 3.7 km).
- In other words "take away the sun" and let us explore the properties of this geometry. Like that...
- But it's a solution that refers to an empty universe ?!
- Take no notice, let's see what we get ...
Study began on the radial trajectories of objects in free fall towards what would be, under these conditions, "a black hole of solar mass" of 3.7 km diameter. The variable t was retained, it was meant to refer to the time experienced by an "exterior observer", a good earthling looking at the sun they had just conjured away. It was discovered that the time of freefall of each test particle, measured according to this time, became infinite. However if we attached a clock to the said particle, it would arrive at the geometric centre of the object in a finite time period.
Theoreticians therefore proposed the following vision :
- This stationary, exterior solution finds a new, providential employment. In effect, gravitational collapse does take place in a very brief period (about one ten thousandth of a second for a destabilised neutron star). However as the phenomenon seems to last for an infinite time to an "exterior observer", a stationary solution can be used to describe an eminently unstationary phenomenon.
If there are no Thrushes, we'll eat Blackbirds....
Starting from this idea, theoreticians began to ask themselves what would happen to matter when it crossed the Schwarzschild surface. And there they found all the horrors mentioned earlier. The particle's time became... pure imagination. The particle's speed exceeded the speed of light. It becomes a tachyon, whose mass is ... imaginary etc., etc.
Some even suggested (and you can find it in many books) that on the interior of the sphere, the variable r transformed itself into time and the variable t into... radial distance.
As Jean Heidmann, cosmologist at Meudon, now retired, used to say :
- When the talk turns to black holes, you have to leave your common sense in the cloakroom...
Under these conditions, if we decide to forget common sense, where is the limit to unreasonableness? How do we decide to build a "physics of the unobservable". This is the case for "dark matter" about which anything and everything is said and written, often at the rate of several dozen papers a day. Nobody seems to have looked into the gemellary model, abundantly developed on my site. However some foreign researchers (China, Japan) seem to have picked up on it well.
There is news in this area. In 88-89 I published three articles in Modern Physics Letters A (reproduced on the site) which launched the idea, unprecedented, of a cosmology in which physical constants could vary, including the sacrosanct speed of light c. The idea was "rediscovered" in 1993. Numerous papers have been published since in very selective reviews such as Physical Review, Classical and Quantum Gravity. There is already quite a large group of "constant variers". Some of them have discovered my work on the Internet site. Many of them were stupefied, even more so by the fact that the work emanated from France, a country which has never got itself noticed through an important innovation in cosmology, or even in astrophysics (fields that are typically German, Russian, American or British). Contact was established in a very cordial manner. The Chinese, not without humour, said that he had to get down his atlas to find the whereabouts of Marseille and had "the impression of discovering an unknown region of the globe".
Why this digression ? Because, in our opinion, the vertiginous pressure increase in the neutron star's core should alter the constants of physics and create a "hypertoric bridge" between the universe and its twin. It is an idea that needs further study. This being said, if help is required in this entreprise, it will most likely come from the "constant variers" who have already crossed the line. For the time being we are the only "gemellarists" but things might not always remain that way.
In our opinion therefore, the gemellary context should completely change the scenario for a destabilised neutron star. However before we are able to propose a challenger model, we must study the classic model of the black hole. That is what is being done in this long paper. Things are not treated "in order". In one section we carefully looked at Kruskal's work, showing the faults in his approach.
Everything is motivated. In 1960 Kruskal had noticed that in the initial model (the "Schwarzschild metric") the speed of light was nil on the sphere in question, the "horizon sphere", alias the Schwarzschild Sphere, and set about curing this "illness".
But how do you work on geometric solutions ? Can others be invented ? The answer is no. I believe that the article shows clearly the arbitrary character of the choice of coordinates. By its essence, a geometric solution is of "invariant coordinates", it does not depend on the coordinates chosen. Imagine a soap bubble. It is a surface. In one sense it is a solution to a field equation which corresponds to the fact that the energy used in tension, to counterbalance a constant pressure inside the bubble, is constant on all its surface. To the question :
- What is the surface that reacts mechanically in way that can support internal overpressure ?
The reply is :
- It's a sphere.
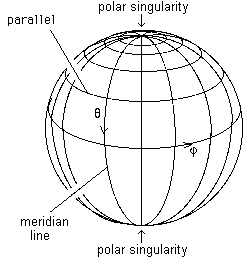
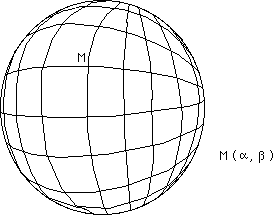
But this sphere, a geometric object, exists independantly of the coordinate system used to identify its points. Now we know that when using a system of meridians and parallels we create polar singularities, apparently singular points whereas in fact they are not. They are singularities induced by the choice of coordinates. In the case of the sphere, by the way, these singularities are inevitable. The figure below shows a sphere and its marking system of latitude and longitude coordinates.
Remark : We can map a sphere, give it a marking system with two parameters using just one pole. See the following figures :
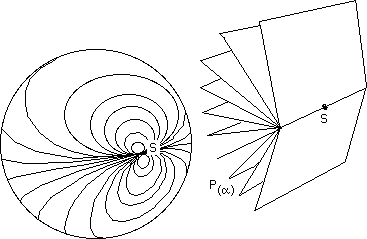
First mark, first family of curves to a parameter a obtained by cutting the sphere in planes through a straight line tangent to one of its points.
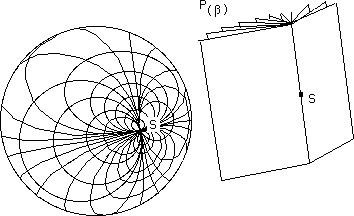
This is combined with the second family of curves obtained bycutting the same sphere along another straight line tangent to the sphere at the same point, for example, orthagonal to the first.
The sphere, thus mapped, seen from another angle which hides its unique singularity.
