Présentation de l'article " Questionable black hole "

    Traduction française :
Des doutes sur l'existence des trous noirs.

    Pour aller directement sur l'article scientifique

    Auteurs :

    Ce travail représente l'aboutissement de dix années d'efforts. Depuis 30 ans les astrophysiciens n'ont qu'un mot à la bouche "trous noirs". Le mot fascine le grand public. De nombreux livres ont été consacrés au sujet. Pourtant les confirmations observationnelles manquent : les trous noirs "brillent par leur absence". Or on sait que le cosmos est vaste. Notre seule galaxie contient au moins 100 à 200 milliards d'étoiles.

    L'existence de certain objets a été révélée par l'observation, celle des quasars, par exemple. On en connaît maintenant plus de quatre mille. Cela ne veut pas dire qu'on sache ce que sont exactement ces objets, comment ils se forment, comment ils évoluent et quelle est leur durée de vie. En fait on ne sait rien sur eux. Ils sont simplement catalogués, comme jadis les "nébuleuses", du temps de l'astronome Messier.

    Apparemment, certains quasars habitent au centre de formations ayant une forme de galaxie. Ces galaxies ont donc "un noyau actif", ce qui veut tout dire et rien dire à la fois puisqu'on ne sait rien de la nature de cette activité, par exemple quelle est la source d'énergie.

    L'astrophysique contemporaine semble se contenter de peu. A la question

    - Qu'est-ce qu'un quasar ?

    L'astrophysicien répondra :

    - C'est le noyau d'une galaxie active.

    Et à la question :

    - Qu'est-ce qu'une galaxie active ?

    Il répondra :

    - C'est une galaxie qui possède un quasar en son centre..

    Plus récemment on a découvert, il y a quelques années, les "flashes gamma", à raison de un par jour. La revue Ciel et Espace titra un jour, en couverture "les flashes gamma : une énigme enfin résolue". Réponse, dans les colonnes du journal : on venait de localiser une petite tache brillante en lieu et place d'un flash gamma qui venait d'être détecté. Entendre donc : résoudre une énigme consiste à savoir que les zone du ciel qui émettent ces flashes sont aussi émettrices de lumière...

        N'est-ce pas un peu .. indigent ?

    Inversement, il existe d'autres objets dont l'existence a été conjecturée, souvent avec pas mal de précision, avant même qu'il soient observés. L'exemple-type est la supernova, décrite dès 1931 par l'astrophysicien américain (d'origine suisse) Fritz Zwicky, lors d'une célèbre conférence donnée au Caltech, USA. Zwicky expliqua à l'époque les étoiles suffisamment massives, dont la masse excéderait disons vingt masses solaires, devraient connaître une fin paroxystique, avec une montée en régime en seulement quelques jours, le phénomène complet s'étalant sur une vingtaine jours. C'était une prédiction tout à fait remarquable, bien qu'elle n'ait pas été prise au sérieux à cette époque. Mais Zwicky, tenace, découvrit les premières supernovæ. On en recense actuellement plusieurs centaines. Même chose pour les étoiles à neutrons, identifiées par la suite aux pulsars (étoiles à neutrons en rotation) et les naines blanches. Là encore le bestiaire, l'espèce compte plusieurs centaine d'individus identifiés.

    Le trou noir a été proposé en tant que réponse à un problème : le devenir d'une étoile à neutrons excédant une certaine "masse critique". Ces étoiles à neutrons dûment identifiées, ressembleraient à d'énorme noyaux d'atomes, sans protons. Pourquoi ces objets sont-ils constitués uniquement de neutrons ?

    On considère l'étoile à neutrons comme ce qui reste du noyau de fer d'une étoile massive, après qu'elle ait explosé. Une étoile massive est une étoile où de nombreux types de réactions de fusion se produisent, au cours de son histoire. Elle finit par produire du fer, qui ne peut alors se prêter à aucune réaction de fusion exo-énergétique. Ce fer, lourd, tombe donc au centre de l'étoile, comme la cendre dans un foyer. Quand l'étoile se trouve soudain en panne de carburant de fusion (ce qu'avait compris Zwicky) elle dégringole sur elle-même à 80.000 kilomètres par seconde (à quelque kilomètres par seconde près, bien sûr). En tombant sur le noyau de fer, ce gaz est fortement comprimé. Non seulement il rebondit dessus, mais au passage de nombreuses réactions de fusion s'y produisent, qui n'ont plus besoin d'être exo-énergétiques, puisque l'énergie vient alors de la contraction brutale de l'étoile sur elle-même. Toutes les espèces nucléaires possibles et imaginables sont alors créées, y compris nombre d'atomes radio-actifs, de durée de vie très variées. On sait qu'en 1987 l'observation de l'explosion de l'étoile Sanduleak, dans le nuage de Magellan, a apporté une confirmation définitive à l'existence de tels phénomènes (à seulement 150.000 années lumière de distance).

    Le phénomène écrase complètement le noyau de fer en disloquant ses atomes. Celui-ci se trouve alors si comprimé sur lui-même que les électrons n'ont plus de place suffisante pour circuler entre les nucléons. Piégés, ils se combinent alors avec les protons en donnant des neutrons et des neutrinos.

    Normalement, quand on comprime un gaz, un phénomène nommé pression s'oppose à cette compression. Cela vaut aussi pour un liquide ou un solide (tout est compressible). C'est ce qui se passe par exemple quand une jeune étoile naît. La proto-étoile une masse de gaz qui se tasse sur elle-même. Mais elle s'échauffe et la force de pression limite sa contraction. C'est un médiocre radiateur et elle devra perdre de l'énergie par rayonnement (infrarouge) avant de pouvoir se tasser suffisamment pour se transformer en véritable étoile. Sauf si sa masse est insuffisante, auquel cas ça deviendra "un gros Jupiter" (cette planète géante continue de rayonner plus d'énergie qu'elle n'en reçoit du Soleil, mais ne se transformera jamais en étoile).

    Quand l'explosion de la supernova comprime le noyau de fer, celui-ci évacue son énergie en émettant une fantastique quantité de ... neutrinos. Là, le scénario change du tout au tout : le refroidissement radiatif est instantané, puisque les neutrinos s'échappent sans difficulté. Donc pas de force de contre-pression. Le bout de fer s'écrabouille lamentablement. Il reste un tas de neutrons, tassés les uns contre les autres, comme des japonais dans leur métro aux heures de pointe.

    Pourquoi une masse critique ? Parce que les neutrons ne peuvent encaisser une pression supérieure à une valeur maximale. Comme des ampoules électriques entassées dans un puits de mine. Au delà d'une certaine hauteur d'ampoules, le verre casse et c'est un nuage de verre brisé qui s'effondre au fond du puits.

    Quand une étoile à neutrons a une masse qui dépasse un peu plus de deux fois la masse du soleil, sa pression à cœur devient trop forte. Les neutrons ne peuvent plus sa supporter. Alors elle est censée s'effondrer sur elle-même sans qu'aucun phénomène physique connu puisse être invoqué pour contrarier cet effondrement, ce "collapse gravitationnel". Perspective angoissante pour un physicien.

    Avant même qu'elle n'implose, une étoile à neutrons est "relativiste", par opposition à un "objet newtonien". Cela se traduit par l'allure des trajectoires de "particules-témoins" à proximité (une masse m quelconque, un atome, par exemple). On sait que le phénomène de courbure de l'espace temps entraîne une précession de l'orbite elliptique de Mercure. Mais cette précession est infime. Par contre, le dessin ci-après, extraits de calculs sur ordinateur, montre la forte précession d'une trajectoire quasi-elliptique autour d'une étoile à neutrons.

    Donc, pas question de décrire une étoile à neutrons avec "du matériel newtonien".

    Le programme de calcul est d'ailleurs assez simple et un jour où j'aurai le temps, je mettrai tout cela sur le site pour que vous puissiez jouer avec, et mettre en outre en évidence le phénomène (ci-après très accentué) de lentille gravitationnelle :

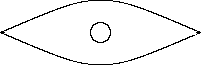
    Ainsi, s'agissant de décrire le destin d'une étoile à neutrons atteignant la criticité, il fallait utiliser une "équation de champ", celle d'Einstein.

    T est un "tenseur" qui décrit le contenu local en "matière énergie". Avant que l'étoile à neutrons n'implose, ce tenseur est nul à l'extérieur et non nul à l'intérieur. La solution géométrique doit donc se déduire de deux équations :

    pour l'intérieur

    pour l'extérieur.

    Le solutions de ce genre d'équations s'appellent "des métriques". Mais peu importe la forme que ces objets prennent. En plus, ce sont des "tenseurs", et avant de comprendre ce qu'est un tenseur, bonjour. Moi, j'ai mis du temps.

    Les soleil est associée à une "géométrie", locale, qui est solution de ces deux équations. La première décrit l'intérieur du soleil et la seconde le vide extérieur. Ceci étant, on ne sait décrire qu'une sorte de "soleil idéal" qui serait une sphère emplie de matière à densité constante. Mais c'est mieux que rien. Ces solution ont des expressions mathématiques que nous n'indiquerons pas. Elles ne vous diraient rien. Chacune a "sa pathologie propre". Appelons rn le rayon de l'astre, de densité constante r. A partir de cette densité r, de la valeur c de la vitesse de la lumière on calcule un premier rayon caractéristique, "R chapeau" :

    La solution géométrique intérieure est "non-pathologique" si et seulement si la valeur du rayon rn est inférieur à cette valeur critique.

  Toujours à partir de ces données, on peut calculer un deuxième rayon caractéristique :

qui est ce qu'on appelle le "rayon de Schwarzschild" Rs. La solution extérieure, qui se réfère au "vide" entourant notre astre de densité constante r et de rayon sera non-pathologique si et seulement si la valeur du rayon rn de l'astre est supérieure à cette longueur caractéristique. En regroupant les deux il faut que :

    La quantité qui est à droite de dépend que de la densité de l'astre (entre 10¹⁵ et 10¹⁶ grammes par centimètre cube). A densité constante, celle de gauche croît comme le cube du rayon r_n de l'astre.

    Ceci vaut pour le soleil, considéré comme un astre de densité constante, en première approximation. Qu'entend-t-on par "pathologies ? Tout : de quantités sous des radicaux qui deviennent négatives, des dénominateurs qui deviennent nuls. On voit donc qu'un astre de densité constante ne peut être décrit par ce type de solution stationnaire que si :

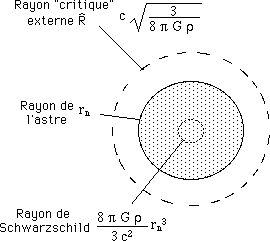
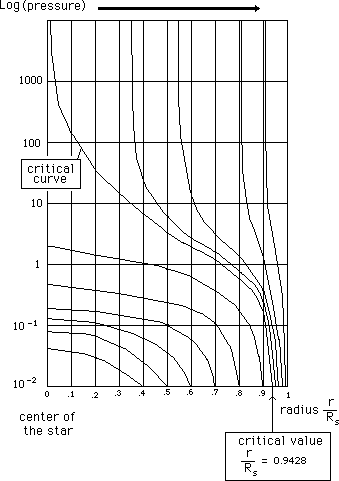
    Le "rayon de Schwarzschild" du soleil vaut 3,7 km : il est bien à l'intérieur de celui-ci (r_n ). Vous pourrez vous amuser à calculer, sachant que son rayon fait 695.000 km la valeur de ce second rayon critique "R chapeau", qui lui est supérieure.

    S'il s'agissait du soleil, le rayon de Schwarzschild (3,7 km) serait, à l'échelle du dessin, quasi ponctuel. Quant au rayon "R chapeau", il sortirait de la feuille. Le dessin ci-dessus se réfère plutôt à une "étoile à neutrons subcritique".

    Comment s'effectue alors la "montée vers la criticité" ? Il suffit d'ajouter des couches de neutrons, en accroissant à densité constante (on assimile l'étoile à neutrons, sinon à un solide, du moins à une goutte fluide pratiquement incompressible ).

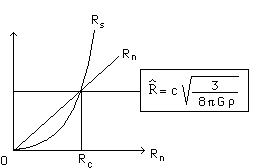
    On obtient les courbes ci-dessus, simplement à l'aide de la formule indiquée. Le rayon de l'étoile augmente, mais le "rayon de Schwarzschild" le rattrape. Et il se trouve que les deux se rejoignent lorsque rn atteint la valeur "R chapeau". Alors, à la surface de l'astre, le quantités sous radicaux deviennent négatives, les dénominateurs deviennent nuls, etc. C'est la traduction mathématique, géométrique, de la criticité. Cela veut dire simplement qu'il est impossible d'utiliser la, ou les deux solutions géométriques raccordées, issues de l'équation d'Einstein avec second membre non nul (intérieur), ou nul (extérieur), pour décrire l'astre. Valeur caractéristique maximale de ce rayon : une vingtaine de kilomètres. Vous en déduirez la valeur de la densité dans l'étoile à neutrons.

    Mais il est une chose peu connue, y compris des "cosmic men", alors que c'est un travail qui date de années quarante : il existe une autre criticité, de nature physique celle-là, qui se manifeste juste avant que le rayon de l'étoile n'atteigne cette valeur. C'est une valeur très proche puis qu'elle n'est que de 5% inférieure. Mais, lorsque le rayon de l'étoile l'atteint, ou, ce qui revient au même, que la masse atteint une valeur double de la masse du soleil, la pression devient infinie au centre de l'étoile, en vertu d'un modèle "TOV" construit dans les années quarante par Tolman, Oppenheimer et Volkov (c'est bien l'Oppenheimer de la bombe).

    Peut-être les scientifiques, comme les autres hommes, ne se posent-il que des questions auxquelles ils pensent pouvoir apporter une réponse. Comment répondre à la question :

    - Que se passe-t-il au sein d'un milieu où, soudain, en un point, la pression devient infinie ?

    Personne ne s'est posé la question, du moins en la formulant de cette manière. Cela n'a attiré l'œil de personne, apparemment. Beaucoup de spécialistes de cosmologie avec qui j'ai discuté ignoraient cet aspect de la chose.

    Revenons à "l'histoire du trou noir". On pourrait se dire : Le phénomène de l'implosion d'une étoile à neutrons déstabilisée est un phénomène instationnaire. Construisons donc une solution instationnaire de l'ensemble des deux équations ci-dessus. Mais on ne sait pas faire, de manière crédible. Alors des théoriciens lorgnèrent sur la "solution extérieure" (celle qui décrit par exemple la géométrie à l'extérieur du soleil et qui devient "pathologique" à son rayon de Schwarzschild, de 3,7 km).

    - Autrement dit "enlevons le soleil" et explorons les propriétés de cette géométrie. Comme ça....

    - Mais, c'est une solution se référant à un univers vide ?!

    - Passons outre, regardons ce que cela donne...

    On s'est mis à étudier les trajectoires radiales d'objets tombant en chute libre dans ce qui serait, dans ces conditions, "un trou noir d'une masse solaire", de 3,7 km de diamètre. On conserva la variable t, censée se référer au temps vécu par "un observateur extérieur", un brave terrien qui observerait un soleil qu'on vient d'escamoter. On trouva alors que le temps de chute libre de toute particule témoin devenait, décompté dans ce temps, infini. Pourtant, si on attachait un horloge à ladite particule, elle arriverait au centre géométrique de cet objet en un temps fini.

    Les théoriciens proposèrent alors la vision suivante :

- Cette solution stationnaire, extérieure, trouve un réemploi providentiel. Le collapse gravitationnel s'effectue effectivement en un temps très bref (de l'ordre d'un dixième de millième de seconde pour une étoile à neutron déstabilisée). Mais comme ce phénomène semble durer, pour un "observateur extérieur", un temps infini, cela permet d'utiliser une solution stationnaire pour décrire un phénomène éminemment instationnaire.

    Faute de grives, on mange des merles....

    En partant de cette idée, les théoriciens se sont alors demandé ce qu'il devait advenir de la matière lorsqu'elle franchissait cette surface de Schwarzchild. Et là ils retrouvèrent toutes les horreurs évoquées précédemment. Le temps propre de la particule devenait... imaginaire pur. La vitesse de la particule excédait celle de la lumière. Elle devenait un tachyon, dont la masse est ... imaginaire, etc... etc....

    Certains suggérèrent même (et cela traîne dans tous les livres) qu'à l'intérieur de cette sphère la variable r se transformait en temps et la variable t en .. distance radiale.

Jean Heidmann, cosmologiste à Meudon, aujourd'hui à la retraite, avait coutume de dire :

    - Quand on parle de trous noirs il faut laisser son bon sens au vestiaire...

    Dans ces conditions, si on décide de laisser tomber le bon sens, où est la limite à la déraison ? Comment décider de construire "une physique de l'inobservable". C'est le cas de la "matière sombre" à propos de laquelle il se dit et s'écrit n'importe quoi, à coup de dizaines de papiers par jour. Personne ne semble s'être penché sur le modèle gémellaire, abondamment développé dans mon site. Cependant des chercheurs étrangers (Chine, Japon) semblent avoir bien accroché.

    Il y a sur ce point, un fait nouveau. En 88-89 j'avais publié trois articles dans Modern Physics Letters A (reproduits sur le site) qui lancèrent l'idée, sans précédent, d'une cosmologie où les constantes de la physique pouvaient varier, y compris la sacro-sainte vitesse de la lumière c. L'idée a été "redécouverte" en 1993. De nombreux papiers ont été depuis, publiés, dans des revues très sélectives comme Physical Review, Classical and Quantum Gravity. Il y a un groupe déjà assez important de "varieurs de constantes". Certains de ceux-ci ont alors découvert mes travaux via le site Internet. Chez beaucoup, cela a été la stupéfaction la plus complête, d'autant plus que ces travaux émanaient de France, un pays qui ne s'est jamais signalé par quelqu'innovation marquante en cosmologie ou simplement en astrophysique (domaines typiquement allemands, russes, américains, anglais). Le contact s'est établi, de manière très cordiale. Le chinois, non sans humour, disent s'être précipités sur un Atlas pour voir où était Marseille "ayant l'impression de découvrir une région inconnue du globe".

    Pourquoi cette digression ? Parce que, selon nous, cette montée vertigineuse en pression au cœur de l'étoile à neutrons devrait altérer les constantes de la physique et créer un "pont hypertorique" entre l'univers et son jumeau. Idée qui reste à étayer. Ceci étant, si de l'aide doit être trouvée dans cette entreprise, elle peut venir a priori des "varieurs de constantes", qui ont déjà franchi ce pas. Nous restons pour le moment les seuls "gémellaires, mais ça ne durera peut être pas éternellement.

    A notre avis, donc, le contexte gémellaire devrait changer totalement le scénario de l'étoile à neutrons déstabilisée. Mais, avant d'être capable de proposer un modèle challenger il fallait examiner le modèle classique du trou noir. C'est ce qui est fait dans ce long papier. Les choses ne sont pas traitées "dans l'ordre". Dans une des sections on a examiné avec soin le travail de Kruskal en montrant les défauts de son approche.

    Tout a une motivation. Kruskal avait constaté en 1960 que la vitesse de la lumière, dans le modèle initial (la "métrique de Schwarzschild") était nulle sur la sphère en question, la "sphère horizon", alias Sphère de Schwarzschild. Il a donc cherché à guérir le modèle de cette "maladie-là".

    Mais comment travaille-t-on sur ces solutions géométriques ? Est-ce qu'on en invente d'autres ? La réponse est non. Je pense que nous avons bien montré dans l'article, le caractère arbitraire du choix des coordonnées. Par essence, une solution géométrique est "coordinate invariant", ne dépend pas des coordonnées choisies. Imaginez une bulle de savon. C'est une surface. En un sens c'est une solution d'une équation de champ qui correspond au fait que l'énergie mise en jeu dans les tensions, pour contrebalancer une pression constante à l'intérieur de la bulle, est constante sur toute sa surface. A la question :

    - Quelle est la surface qui réagit mécaniquement de manière à supporter une surpression interne ?

    La réponse est :

    - C'est une sphère.

    Mais cette sphère, objet géométrique, existe indépendamment du système de coordonnées qu'on utilise pour y repérer ses points. Or on sait qu'en utilisant par exemple un système de méridiens et de parallèles on crée des singularités polaires, des points apparemment singuliers, alors qu'ils ne le sont pas. Ce sont donc des singularités induites par le choix des coordonnées. Dans le cas de la sphère, d'ailleurs, ces singularités sont inévitables. 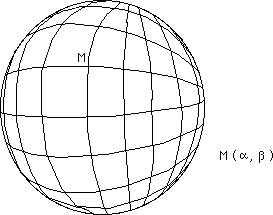Ci-après une sphère munie de son système de repérage par les coordonnées latitude-longitude.

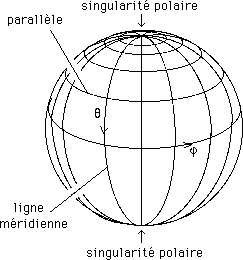
    Remarque : on peut cartographier une sphère, la doter d'un système de repérage à deux paramètres, en n'utilisant qu'un pôle unique. Voir les dessins ci-après :

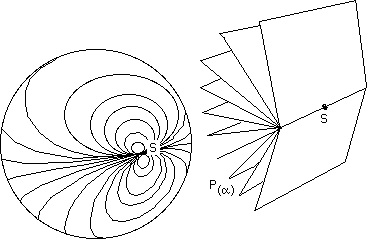
    Premier repérage, première famille de courbes à un paramètre a obtenues en coupant la sphère par des plans passant par une droite tangente en un de ses points.

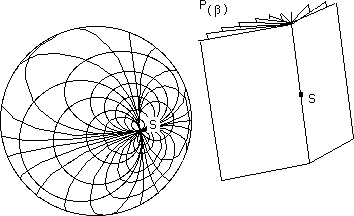
On combine avec une seconde famille de courbes obtenues en coupant cette même sphère par d'autres plans passant par une autre droite tangente à la sphère au même point, par exemple orthogonale à la première.

...On combine avec une seconde famille de courbes obtenues en coupant cette même sphère par d'autres plans passant par une autre droite tangente à la sphère au même point, par exemple orthogonale à la première.