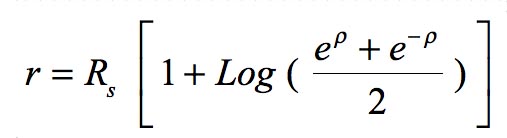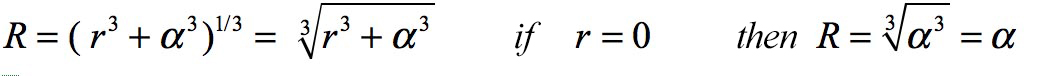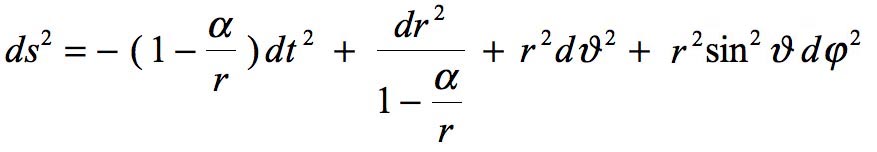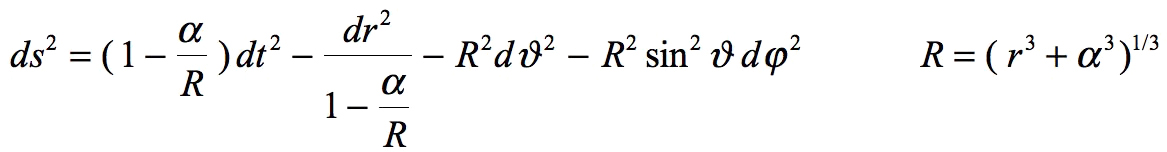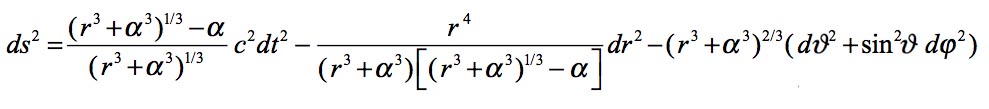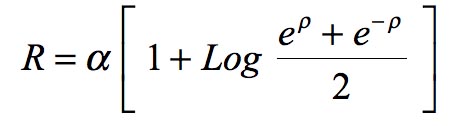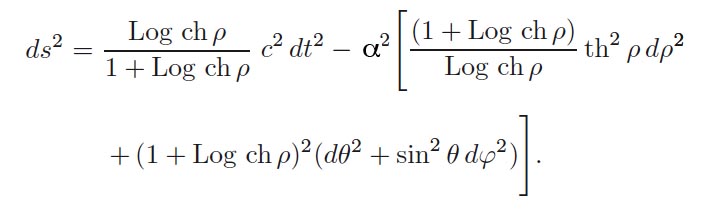Report of the 3rd Karl Schwarzschild Meeting

Report of the 3rd Karl Schwarzschild Meeting
FIAS, Frankfurt, Germany
24–28 July 2017

I've just come back from the 3rd Karl Schwarzschild Meeting on gravitational physics and the gauge/gravity correspondence, held in Frankfurt, Germany, at the prestigious FIAS (Frankfurt Institute for Advanced Studies).

I was very hesitant about the content of my poster and finally decided to present my system of two coupled field equations, heart of the Janus Cosmological Model.

A text which did not fit well with the central theme of the symposium, focused on "the physics of black holes". This is a topic I intended to address later, but a paper I published in 2015 in Modern Physics Letters A:

Petit, J.-P.; d'Agostini, G. (21 March 2015). "Cancellation of the central singularity of the Schwarzschild solution with natural mass inversion process". Modern Physics Letters A. 30 (9): 1550051. doi:10.1142/S0217732315500510.

was the closest thing I had already published though peer review. As there was a blackboard next to my poster, I wrote the main lines of this paper:

It attracted a lot of attention. Conference delegates took pictures and a crowd formed. A sixty-year-old senior researcher immediately expressed his skepticism about the fact that all singular aspects of the metric solution found by Schwarzschild in 1916 (which supports the theory of the black hole) could be eliminated using a simple change of variable. Since he was not wearing a badge, unlike others, I concluded he should be a member of the FIAS, the Frankfurt Institute for Advanced Science, hosting this symposium. Here is this change of variable:

Some critic, at last! To make things even clearer I quickly wrote all the details of the calculation on a sheet of paper that I gave to my expert. He took the paper, walked away a bit, sat down on a chair and buried his nose in the equations for a quarter of an hour.

Everyone waited for his verdict. He finally gave my paper back with a nod of agreement. The greatest perplexity could be read on his face. I think he must have said: "I've never seen this thing anywhere before. Obvioulsy this French guy has made some mistake somewhere that I have missed for now. I'll find it later."

I tried to hook him up to this problem, which raises the question of the interpretation of Karl Schwarzschild's 1916 result (the symposium was called the "Karl Schwarzschild Meeting"!). I asked him if he had read the original paper published in the Proceedings of the Prussian Academy of Sciences, detailing what is now called the "exterior Schwarzschild solution":

Schwarzschild, K. (13 January 1916). "Über das Gravitational eines Massenpunktes nach der Einsteinschen Theorie". Sitzungsber. Preuss. Akad. Wiss. Berlin (Phys.-Math.) 1916. 189–196
translated in English as:
Antoci, S.; Loinger, A. (12 May 1999). "On the gravitational field of a mass point according to Einstein's theory". arXiv:physics/9905030 [physics.hist-ph]

As well as his second paper, published a few weeks later (less than three months before his death), the "interior Schwarzschild solution":

Schwarzschild, K. (24 February 1916). "Über das Gravitationsfeld einer Kugel aus incompressibler Flüssigkeit nach Einsteinsechen Theorie". Sitzungsber. Preuss. Akad. Wiss. Berlin (Phys.-Math.) 1916. 424–434
translated in English as:
Antoci, S. (12 May 1999). "On the gravitational field of a sphere of incompressible fluid according to Einstein's theory". arXiv:physics/9912033 [physics.hist-ph]

He admitted he had never read them (!) adding:

— Do you read German?

— No, but I have read English translations, relatively recent admitedly (1999) for century-old papers. I have these documents in my laptop. Do you agree we look at them together? There is also a very important text published by David Hilbert in December 1916, taking over Schwarzschild's work after his death.

Hilbert, D. (23 December 1916). "Die Grundlagen der Physik (Zweite Mitteilung)". Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, (Math.-Phys.). 53–76.
translated in English as:
Renn, J. (2007). "The Foundations of Physics (Second Communication)". The Genesis of General Relativity, Vol.4: Gravitation in the Twilight of Classical Physics: The Promise of Mathematics. Springer. 1017–1038.

He eluded, adding that he did not know this other article neither (!)

Actually, what I discovered in Frankfurt is that the black hole men simply do not know the founding texts from which the works they intend to develop have been conceived. In a masterly lecture in front of all the congressmen, Juan Maldacena, a "figure" of modern developments of the black hole theory, began saying (as reproduced in the symposium brochure):

Juan Maldacena

— The Schwarzschild solution has confused us for over a hundred years and it has forced us to sharpen our views on space and time. It has lead to a sharper understanding of Einstein's theory. Experimentally, it is explaining several astrophysical observations. Its quantum aspects have been a source of theoretical paradoxes that are forcing us to understand better the relation between spacetime geometry and quantum mechanics.

Concretely, what's the point?

First there was the "discovery" of the "Hawking radiation". In fact, all this is based on the idea of a union between General Relativity and Quantum Mechanics. We know such a marriage has never been consummated (gravitation refuses to be quantified, which would lead to the description of a graviton, a spin-2 particle, still AWOL).

Our modern theorists are convinced such a fantasy is a true reality. It is indeed by invoking a quantum phenomenon near the event horizon that Hawking "demonstrated" that the black hole could lose energy, "radiate". This immediately lead to the black hole information paradox. Indeed, in these objects named black holes, any structure is supposed to be crushed. Anything would totally disappear. So black holes would be "machines destroying information". Maldacena then outlined the progress made about "black-hole thermodynamics". In particular, he pointed out that "the entropy of black holes was shown to be proportional to their surface".

In short, in the last few decades all the attention of theorists has focused on how circumventing this information paradox. You've probably heard of a "firewall" and other things like that. In his last work, Maldacena invokes a new "magic word": entanglement. A concept derived from quantum mechanics and the famous Einstein-Podolsky-Rosen paradox (EPR paradox) which I described in my video JANUS 6 (at 14:04). In this famous experiment, two emitted photons are "entangled." In short, according to Maldacena, "entanglement" brings all the answers. This, plus a pinch of string theory.

Such a speech is the very best of the theory in 2017.

Participants at the conference obviously referred to the JANUS videos (see the whole playlist here). Thanks to Julien Geffray's great work, videos were translated in English with subtitles, six of them being already translated at the opening of the symposium (JANUS 14 to 19). And it is there that we realized that subtitling in good English is something absolutely indispensable to be heard outside of France. I can't provide a translation in bad English: foreign Internet users would zap immediately. Geffray, who has been following my work for 20 years and fully masters the language of Shakespeare, was the only one able to ensure this subtitling work, very delicate, taking 2-3 days of work for each video. This represents 15,000 to 20,000 characters per video, with a text including a lot of specific jargon to translate, the difficulty of visually organizing and calibrating these subtitles to the nearest tenth of a second, as well as the creation of cards pointing to my published papers and science comics.

Seeing the impact on non-francophones, I realized that I should have all the Janus series subtitled in English. We renegotiated the price to expand the translation further, but the budget is still high for 20+ videos.

Internet users answered the call and made donations through PayPal. This money allows me to travel abroad and attend international conferences (inscription fee, travel and stay expenses) as well as this video subtitling work. Let me add that I will continue to produce these videos at a rate of two per month (yes, there will be also a Janus video about quantum mechanics). It is, in my opinion, well invested money because if the texts on the websites often end up in oblivion, it is not the same for videos, which will continue without limitation of time and which are the modern communication tool par excellence.

Forecast budget until Spring 2018 (subtitling + symposia): 20,000 euros

Making truth emerge, has a price.

If the money sent by Internet users (huge thanks to them!) is enough to ensure my presence in the next few symposia (the Schwarzschild Meeting, Frankfurt; then COSMO-17, Paris…) I will need additional help to deal with these subtitling costs and subsequent conferences.

Impact of these videos: reactions of young researchers at the Schwarzschild Meeting. One of them, an Italian, ended up saying to me:

— I saw your papers about your Janus cosmological model (he had the expertise to appreciate the content). I am looking at how you are welcomed here. How can you expect these people to do anything but turn their back on you? What you are proposing is to destroy the very basis of their work!

The contact with this young man was established and is maintained. He works in Italy on Modified Newtonian dynamics. It is a first seed planted. If I continue to "chat up in international conferences", there will be others in the younger generation and probably not among those who have established their notoriety on the fantastic works I have mentioned.

Some of these young people shall eventually say: "I don't really believe in this MOND theory, what if I try to see where the ideas from this French physicist are leading me?" These contacts and exchanges will be facilitated by the fact that these young researchers can see the videos then the papers about the Janus model when they meet me.

In Frankfurt, most of the presentations were centered on "the physics of black holes", about "what you might observe, if you could observe it…" Adding this new idea of a "holographic universe" to it (I will have to create a video explaining what a hologram really is). One woman explained that "we should not be afraid of cosmic strings". Another showed how pairs of mini black holes could form during the inflation phase of the cosmic expansion. Let's add stories related to string theory, to "brane collisions". I was practically the only one to distinguish myself, proposing works and results… able to be confronted with observations.

If I want to wake the cosmological community up, to react, I must attack their beloved child, the black hole, which I did not expect to do until much later. But the climate at the Frankfurt meeting led me to correct the situation, so the title of my next video will be:

JANUS 21: The black hole, born of a misinterpretation of the solution found by Karl Schwarzschild in 1916

That will also be my words at the COSMO-17 international conference in Paris. It will not be about proposing an alternative model for the black hole (not yet), but to claim:

— As is, the model of this object called "black hole" is inconsistent, because it does not correspond to the solution found by Karl Schwarzschild in 1916, and I show it.

German mathematician Karl Schwarzschild
died in Potsdam on May 11, 1916 at age 43
three months after the publication of his solutions to Einstein's equations

The solution was found in 1916 by Schwarzschild and published as:

In this first paper, Schwarzschild perfectly defines a coordinate r as a "polar coordinate":

But he introduces what he calls an auxiliary quantity R, and it is through it that he expresses his famous "exterior" solution in January 1916:

No need to be a mathematics major to see that, insofar as the variable r chosen by Schwarzschild (as he defined above) is strictly positive, the intermediate quantity R is not free but has a lower limit α:

Schwarzschild died in Potsdam on May, 11 1916 at age 43, only a few months after this first publication.

Resuming this work in a communication made in December 1916 at the Göttingen Academy of Sciences, great German mathematician

David Hilbert, 54 years old in 1916

considers this method of expressing the solution as being uninteresting, which in this case sends the singularity (in R = α) to the origin, in r = 0.

Hilbert's communication is dated 23 December 1916 (Schwarzschild passed away in May):

Actually, Hilbert was already working hard on the theory of general relativity, the title of his paper being "The Foundations of Physics". People often tend to think Einstein was the physicist and Hilbert the pure mathematician. Indeed, Hilbert didn't like much the technical aspects of science. On day, he was asked to replace his colleague mathematician Felix Klein, who was ill, to give a lecture in front of student engineers. Hilbert began his talk with a jest:

— One hears a lot of talk about the hostility between scientists and engineers. I don't believe in any such thing. In fact I am quite certain it is untrue. There can't possibly be anything in it because neither side has anything to do with the other.

But not only engineers were hauled over the coals. There is also this famous quote of him:

— Physics is becoming too difficult for the physicists.

Hilbert's work in mathematics is actually considerable. But if you have the curiosity to refer to this historical document, you will discover that he tries to lay the foundations of a highly mathematized physics (a true mathematical physics). In comparizon to his quip at the school of engineering, Hilbert changed his mind a bit, perhaps following his meeting with Einstein, or more generally following exchanges with the great physicists of the time. Of course, when it comes to bringing his own contribution, he thinks big straightaway. This paper lays the basis for a "Lagrangian approach" to the entire physics, that is to say, both gravitation and electromagnetism. In this writing it is clear that Hilbert aims to regroup in this approach "all the physics of the time" in what will later be called a "unified field theory", a work Einstein will also attempt in vain to complete for the rest of his life. The project failed, because the two formalisms cannot be included together with only four dimensions. As well explained by Jean-Marie Souriau in 1954, chapter 7 of his excellent book "Geometry and Relativity" (sadly only published in French, but now freely available), electromagnetism can be included in general relativity using five dimensions, adding the "Kaluza 5th dimension".

When Hilbert publishes this 22-page paper, 23 December 1916, it is by no means an improvisation after Schwarzschild's papers, but the second part of a large communication presented in November 2015, previoulsy withdrawn, Hilbert considering it insufficiently constructed. So he gradually added various developments for a year, as well as Schwarzschild's non-linear solution of Einstein's field equations, which had been published in the meanwhile.

Whatever it be, the addition of Schwarzschild's solution is clearly presented by Hilbert as an insignificant point in his own larger work.

Everything lays in the following excerpt:

Hilbert introduces four coordinates w₁, w₂, w₃, w₄, immediately stating that the first three (the space coordinates) can be expressed as he does, using polar coordinates. To the extent that he thinks about this problem of the gravitational field around a mass point, as falling within a "central symmetry" (zentrischsymmetrisch), this seems to go without saying, according to him:

In the last line he even pushes things further, writing that his term G(r) is identified to the square of this "radial distance".

Then everything follows. And generations of scientists will reproduce this approach in hundreds of books. By the way, here is how he handles his time variable l:

With Hilbert, time is a pure imaginary quantity!

It is his interpretation of Relativity.

In his equation (45) shown above, he just shows the "bilinear form" but here we discover the historic choice of the spacelike metric signature ( + + + – )

This writing focuses the attention on the tangible, real part of space-time: space (affected by three plus signs).
Whereas time is imaginary (thus has a minus sign when squared). Incidentlaly, the unit length s also becomes imaginary, as well as what is called "the proper time". Normal: with Hilbert, anything belonging to time must be imaginary.

He says he obtains Schwarzschild's result (except for the inversion of signs) which should then be written:

Yet, there is a difference: with Schwarzschild, this is not written with the letter r but with the letter R:

Both have a different meaning. But Hilbert doesn't pay much attention to this detail, because it is ovious to him (and it was true at the time) that in astronomy r is always much larger than α (which will later be called the "Schwarzcshild radius").

To make their fundamental difference appear, Let us explain this solution, as Schwarzschild himself might have done if he had lived a little longer. We get:

But he didn't, as the non-explicit form seemed sufficient to him. Remember Schwarzschild's goal in his paper was to explain the precession of the perihelion of Mercury, to find Einstein's prior linearized results, with a non-linear solution to his field equations.

This metric is regular for any value of r > 0.
When r = 0 the coefficients of the two first terms also become zero. I'll explain further the interpretation of this point.

Yet Hilbert adds only a short note about this work (as he was aware of Schwarzschild's death, a simple condescendant footnote as a funeral oration seems a bit stingy):

Translation :

— To transform the locations r = α to the origin, as Schwarzschild does, is not to be recommended in my opinion; Schwarzschild’s transformation is moreover not the simplest that achieves this goal.

The coordinate r = α was for Hilbert a "true singularity". However, it was later shown it was a "coordinate singularity" which could be eliminated by a change of variable.

It is known such metric solutions can be expressed in any choice of coordinate system. It is a fundamental property of solutions of the Einstein field equations. The choice of this or that system is the physicist's choice. This involves giving a physical interpretation to these coordinates. But the theoretical results then have to be confronted with observation, i.e. to calculate trajectories of particles along geodesics, orbiting within the gravitational field created by such a "mass point". That's what they did at the time.

Classically, the variable R is assimilated to a polar coordinate, which then could be eliminated. It is shown that these geodesic trajectories are inscribed in planes. The solution can then be expressed as a function:

Then comparing the curves obtained with observational data, we conclude:

– These trajectories are "quasi-conical" with a focus in R = 0.

– In the usual conditions of planetary astronomy, elliptic trajectories are very close to ellipses, the small difference being what is called the "advance" (or "precession") of the perihelion.

When R ≪ α the quantities r and R are practically identical. Schwarzschild makes the point in his paper (more readable in the translated version):

Apart from the choice of different signatures, we can say the solutions of Schwarzschild or Hilbert (as well as the linearized solution proposed by Einstein) are similar: they lead to almost identical results regarding planetary astronomy. Thus, whether opting for Hilbert's radial variable r or Schwarzschild's variable R, the theoretical results are in agreement with "reality".

The Sun radius is 700,000 kilometers. Schwarzschild calculated its length α (i.e. what will be later called "the Schwarzschild radius") which is 3 kilometers, located much inside the star. Assimilating this sphere with a point represents an approximation of only four millionths.

It is also worth noting – but I will detail this in a next video – that Schwarzschild not only provided the "exterior" solution but also built the "interior" solution (describing the geometry inside a sphere of constant density) in a second paper, published one month later:

It is only nowadays with objects such as neutron stars that a problem arises, about the geometrical and physical representation of objects where "the distance variable" is no longer negligible at all with respect to the Schwarzschild radius. But then, which variable should be chosen: that of Hilbert or that of Schwarzschild?

Theorists then proposed to give a physical nature to this exterior solution, and said that it describes an object they called "black hole". Geometrically, it is necessary to produce an answer:

– according to Schwarzschild's representation, for what happens where r = 0

– according to Hilbert's representation, for what happens where R < α (the "interior" of the black hole)

I emphasis the second question does not arise in Schwarzschild's representation: you don't have to wonder what happens to mass points falling "beyond" α, since such an "interior"... does not exist.

On the other hand, in Hilbert's representation, if this "interior" really exists, it is very strange: the signature of the metric is altered, which makes our modern theorists say: "inside, r becomes time and t becomes the radius".

In this peer-reviewed paper:

I indicated another choice of coordinates, derived from the Schwarzschild solution through the following change of variable:

which leads to a presentation of the metric solution in the form:

It is then regular, whatever the values of the variables, except for the fact that the first term is zero at the origin. The associated geometry is then interpreted considering such a metric describes a passage connecting two Minkowski spacetimes with PT-symmetry, the junction being performed through a throat sphere, of perimeter 2πα. Along this sphere, the determinant is zero, which reflects the double inversion of space and of the arrow of time, when crossing this surface.

Using the metric in the form given by Schwarzschild as a solution of the field equations, expressed with the coordinates (t, r, θ, φ), we could wrongly think at first that the throat sphere is reduced to a single point, similar to the apex of a cone: the point r = 0. But it would be attributing a "dimensional" value to this quantity, which is nothing but a "space marker". A space marker in differential geometry is simply a number allowing to locate some points. The only true distances, real lengths having a meaning, are those calculated with the metric. Such lengths, denoted with the letter s, are invariant whatever the coordinate system chosen (when you consider two identical paths described by two different coordinate systems).

The spherical symmetry property of the solution makes it possible to consider fixing three of the four coordinates (t, r, φ) and to make a revolution of 2π according to the θ coordinate. The throat sphere in Hilbert's representation corresponds to R = α. If t = constant, φ = constant and this turn is performed according to θ, the result is 2πα, the perimeter of a great circle on the throat sphere.

Let's repeat this operation in my own representation (t, r, θ, φ). The throat sphere then corresponds to ρ = 0. The turn along the θ coordinate returns the value 2πα.

What is more surprising is that, when opting for Schwarzschild's representation where the throat sphere corresponds to the value r = 0 we get this length 2πα too! This is very disturbing, because "turning around the point r = 0" gives a non-zero length! This is because r… is not a point! It is a disconcerting aspect of differential geometry and the representation of objects by their metric.

This thought experiment should make you understand that you must no longer consider r as a "dimensional" length. It is precisely because everyone imagines r as a "radial distance" that the confusion arises.

In fact it is even the word "dimension" that brings confusion. Instead of saying "we will locate the points in this geometric object with a set of dimensions" we should say:

— We will locate the points in this geometric object using space markers:

(x⁰, x¹, x², x³)

But even the letter x could be misleading. To totally cancel the erroneous idea that r would be some variable radial distance down to a central point, the space marker should be defined by a neutral Greek letter, like β or ζ:

(ζ⁰, ζ¹, ζ², ζ³)

Let's go back to this general concept of metric. In mathematics, in geometry, what is it?

The Earth is not flat. It is a sphere. This is a problem for cartographers. If we look at continents on a globe, everything's fine. But how to map a curved world onto flat sheets of paper, planar supports, how to proceed? Several maps are established and gathered as an atlas. Neighboring maps can be related to each others by adjusting the correspondence between their meridians and parallels.

More generally, it is possible to map any surface using such a technique. A car body, for example. Each planar element of this atlas corresponds to a local metric description. Mathematicians and geometers have extended this concept considering atlases made of non-Euclidean elements. Imagine a world where paper does not exist and where people would use supports in the form of dried leaves, shaped as portions of a sphere that can be stacked up, forming a strange curved atlas. Anyhing could be mapped like that, step by step (including a plan!).

Such a technique does not entail any constraint
regarding the topology of the object being mapped.

Choosing to shape the object described by the Schwarzschild metric using "polar coordinates" implicitly represents a strong hypothesis on its topology.

In the following, the idea is that the metric solution contains its own topology and that we are not free to choose it. We then drop completely the classical approach of maps constituting an atlas, imagining the object is described only by its metric, expressed in a set of coordinates "that goes well" i.e. which is in agreement with the topology implicitly related to its metric solution. The common thread being:

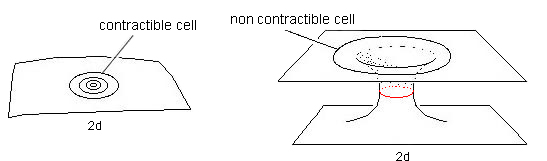
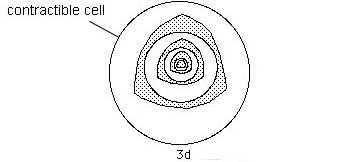
– The unit length s must be real everywhere.

– And its corollary: the signature of the metric is invariant.

On the basis of these comments and suggestions, one can then question the classical model of the black hole, burdenned with its multiple pathologies. Is that not a consequence of the way Hilbert interpreted this geometry? Bearing this chimera known as "the interior of the black hole", which is accessed through "Kruskal's analytic continuation" about which Maldacena, in his conference lecture, said that "it allows to extend the solution to the whole spacetime". The fact is, black hole men have an a priori about the topology of the object they study. How that?

Topologically, let's consider a 2D surface. Draw a closed curve, then try to reduce the perimeter of this curve to zero. There are two scenarii:

– Either this perimeter can be decreased down to zero.

– Or a minimum limit is reached.

This can be illustrated in the following drawing:

If a 2D inhabitant of this surface was asking us:

— What is at the center of the circle?

We could only answer that his question is meaningless, as these circles have no center.

If we switch to a 3D world, such contractibility would appear as the possibility of deforming a sphere by decreasing its area down to zero:

If this operation can complete successfully, then this sphere has an "inside" and a "center".

But a 3D space is not necessarily contractible. If it is not, then in some region (the surface having the topology of a 2-sphere) the foliation of this space through concentric neighboring spheres (i.e. like peeling an onion) will reach a minimum surface. Then, if we try to continue folliating, the surface will grow again, because the minimum area we've just crossed was actually a throat sphere.

It is no longer possible to draw such a thing in 3D, but referring to the previous 2D figure, we shall see that on the right-hand side, the minimum value is a throat circle (in red). All this can be extended to a 3D hypersurface and a hypersurface with any number of dimensions.

Praising Joseph Kruskal "who allowed us to extend the solution to the whole spacetime" Maldacena does not realize (like thousands of others before him) that he unconsciously makes a hypothesis on the topology of the 4D hypersurface he talks about: the "space-time".

Yet this attempt ends in the alteration of the metric signature, going hand in hand with the transformation of the unit length into a pure imaginary quantity. This simply expresses the "answer" provided by the formalism:

— Watch out! You are outside of the hypersurface!

In fact he wants to explore a portion of spacetime that does not even exist, much like a geometrician who would construct an analytic continuation to study the properties of the tangent plane to a torus… near its axis, like some Mad Mechanic who, in the world of Alice in Wonderland, would endeavor to stick a patch on the inner tube of a tire in the area located near the axis of the wheel…

If I'm right, so much paper, ink and gray matter (including quantum gray matter) consumed for decades to describe an object that does not exist, et tout ce qu'il implique, comme les propriétés d'une "singularité centrale"! One may wonder why all this has apparently gone completely unnoticed for a whole century. May historians of science provide us with the answer. Let's say that with his fantasy of an imaginary time, Hilbert conveyed the idea of a spacelike signature (– + + +) which means that, perhaps, nobody thereafter became concerned that the square of the unit of length changed sign. But it is wrong saying that it is only a question of "convention".

However, Schwarzschild (and Einstein) had opted for a timelike signature (+ – – –) as can be seen from Schwarzchild's paper:

Conversely, by fixing the sign of the terms referring to angles, Hilbert implicitly locks the signature to (– + + +) :

Physicists, students and engineers who wish to explore these issues can download below the English translations of the various articles cited in this page, including the historical papers originally published in German a thousand years ago. They have probably never been read by our modern black hole men, who seem to have lost contact with reality, building an astrophysics without observation, resulting from mathematics without rigor.

• Historical papers:

Frank, Ph. (1916) in Jahrbuch über die Fortschritte der Mathematik. 46: 1296.
translated in English as:
Antoci, S. (2003). "Appendix A: Frank’s review of Schwarzschild's 'Massenpunkt' paper" in "David Hilbert and the origin of the Schwarzschild solution". Meteorological and Geophysical Fluid Dynamics. Bremen: Wilfried Schröder, Science Edition. arXiv:physics/0310104.

Droste, J. (1917). "The field of a single centre in Einstein’s theory of gravitation, and the motion of a particle in that field". Proceedings of the Koninklijke Nederlandse Akademie Van Wetenschappen, Series A. 19 (I): 197-215. (Communicated by Prof. H. A. Lorentz at the KNAW meeting, 27 May 1916).
Reprinted (2002) in
General Relativity and Gravitation. 34 (9): 1545–1563. doi:10.1023/A:102074732.

Weyl, H. (1917). "Zur Gravitationstheorie". Annalen der Physik. 54 (18): 117–145. doi:10.1002/andp.19173591804.
translated in English as:
Neugebauer, G.; Petroff, D. (March 2012). "On the theory of gravitation". General Relativity and Gravitation. 44 (3): 779–810. doi:10.1007/s10714-011-1310-7.

• To go further:

Abrams, L. S. (November 1979). "Alternative Space-Time for the Point Mass". Physical Review D. 20 (10): 2474–2479. doi:10.1103/PhysRevD.20.2474.
+ correction:
Abrams, L. S. (April 1980). "Erratum: Alternative space-time for the point mass". Physical Review D. 21 (8): 2438. doi:10.1103/PhysRevD.21.2438.
arXiv:gr-qc/0201044.

Abrams, L. S. (2001). "Black Holes: The Legacy of Hilbert's Error". Canadian Journal of Physics 67 (9): 919–926. doi:10.1139/p89-158. arXiv:gr-qc/0102055.

Antoci, S.; Liebscher, D.-E. (2001). "Reconsidering Schwarzschild’s original solution". Astronomische Nachrichten. 322 (2): 137–142. arXiv:gr-qc/0102084.

Antoci, S. (2003). "David Hilbert and the origin of the Schwarzschild solution". Meteorological and Geophysical Fluid Dynamics. Bremen: Wilfried Schröder, Science Edition. arXiv:physics/0310104.

Petit, J.-P. (2017). "The Janus Cosmological Model" (Youtube playlist, subtitled in English).
See also this PDF file listing the video content.